三角関数の加法定理 sin(α ± β) = sinαcosβ ± cosαsinβ cos(α ± β) = cosαcosβ ∓ sinαsinβ tan(α ± β) = tanα ± tanβ 1 ∓ tanαtanβ まずは,この定理が成り立つことを確かめたいと思います。 証明にはなりませんが,イメージをつかむために α , β , α β がいずれ正弦定理を理解するために前提となる事柄 1 「正弦」とは三角関数のうちの sin θ の値のことで、正弦定理を使うためには 0 °~ 180 ° の三角関数の値が言えなければなりません。 実際に、宙で暗記して言えなければならなのは次の9つの値だけです。 三平方の定理を使って直角三角形の辺の長さを計算したい! どうも、Drリードだぞい。 中3数学では、 三平方の定理(ピタゴラスの定理)を勉強してきたよな? 簡単に復習すると、 直角三角形の直角をはさむ2辺の長さをa、b、斜辺の長さをcとすると、
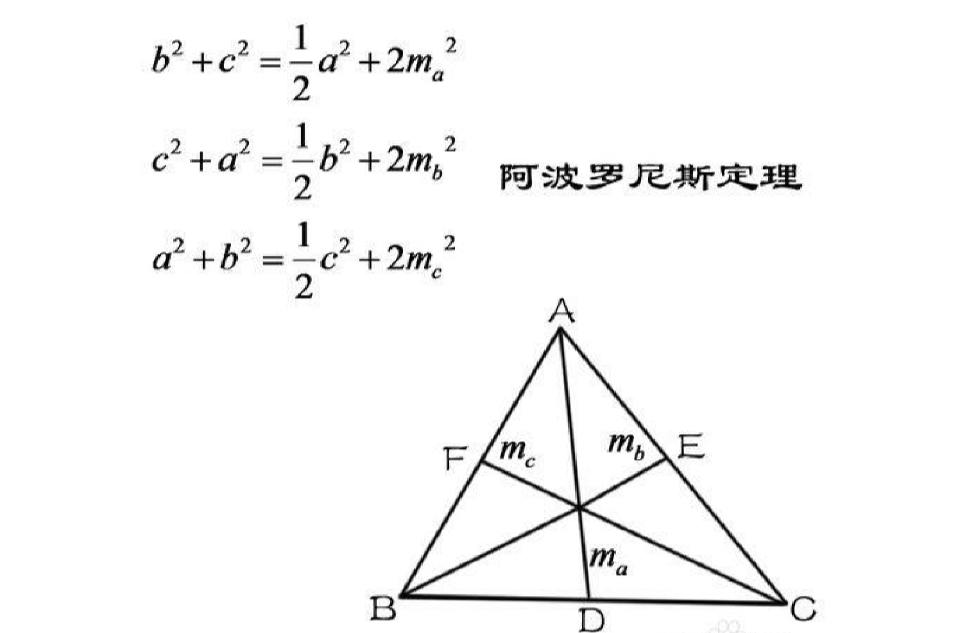
三角形中線定理 中線定義 性質 中線定理 定理證明 推論 中文百科全書
三角定理
三角定理-正弦定理 三角形の各辺 a , b , c と各角 A , B , C の間に以下に示す関係がある. a sinA = b sinB = c sinC a sin A = b sin B = c sin C この関係を, 正弦定理 という. 三角形の 外接円 の半径を R R とすると, 正弦定理 は, a sinA = b sinB = c sinC = 2R a sin A = b sin B = c sin C = 2正弦定理(The Law of Sines)是三角学中的一个基本定理,它指出"在任意一个平面三角形中,各边和它所对角的正弦值的比相等且等于外接圆半径的2倍",即a/sinA = b/sinB =c/sinC = 2r=D(r为外接圆半径,D为直径)。 正弦定理的公式: 在任意 ABC中,角A、B、C所对的



1
三角比6|正弦定理の使い方を具体例から考えよう 三角比を学ぶことで正弦定理と余弦定理という三角形に関する非常に便利な定理を証明することができます. だということは容易に想像が付きますね( 余弦定理 は次の記事で扱いますタレスの定理(タレスのていり、英 Thales' theorem )とは、直径に対する円周角は直角である、つまり、A, B, C が円周上の相異なる 3 点で、線分 AC が直径であるとき、∠ABC が直角であるという定理である。 ターレスの定理、タレースの定理ともいう。 歴史 古代ギリシャの哲学者、数学者タレス三角関数の数々の公式の親となる重要な定理です.この単元の最重要定理と言っても過言ではないかもしれません. 3つの証明と演習問題を用意しました. 目次 1: 三角関数の加法定理 2: 加法定理の3つの証明方法と証明 3: 例題と練習問題
中点連結定理 a b c m n abcの2辺ab, acの中点をそれぞれm, nとすると mn//bc, mn= 1 2 bcとなる。 定理の証明 amnと abcにおいて ∠aは共通(1) mはabの中点なのでamab=12 nはacの中点なのでanac=12 よってamab=anac=12(2)三平方の定理の4通りの美しい証明 レベル ★ 基礎 平面図形 更新日時 三平方の定理(ピタゴラスの定理): ∠ C = 9 0 ∘ \angle C=90^ {\circ} ∠C = 90∘ であるような直角三角形において, a 2 b 2 = c 2 a^2b^2=c^2 a2 b2 = c2正弦定理を三角形の面積と関連付けます。 ※ 図は Markdown に SVG を直接記述しています。詳細はこちらをご参照ください。 正弦定理 図 1 A B C 2R a b c 教科書でよく見る形の正弦定理は、円の直径との関係を含んだ形で記述されます。
余弦定理 三角形の各辺 a , b , c と各角 A , B , C の間には以下に示す関係がある. a2 =b2c2−2bccosA b2 =c2a2−2cacosB c2 =a2b2−2abcosC a 2 = b 2 c 2 − 2 b c cos A b 2 = c 2 a 2 − 2 c a cos B c 2 = a 2 b 2 − 2 a b cos C この関係を 余弦定理 という.三平方の定理 自動計算サイト 三平方の定理による辺の長さの計算です。 三平方の定理は、 直角三角形の三辺をa,b,cとする。 斜辺 (最も長い辺)をcとすると、 c² = a² b² が成り立つ というものです。 別名ピタゴラスの定理とも呼ばれます。 全等三角形定理 天奇生活 字体: 大 中 小 1、三组对应边分别相等的两个三角形全等;2、有两边及其夹角对应相等的两个三角形全等;3、有两角及其夹边对应相等的两个三角形全等;4、有两角及其一角的对边对应相等的两个三角形全等;5
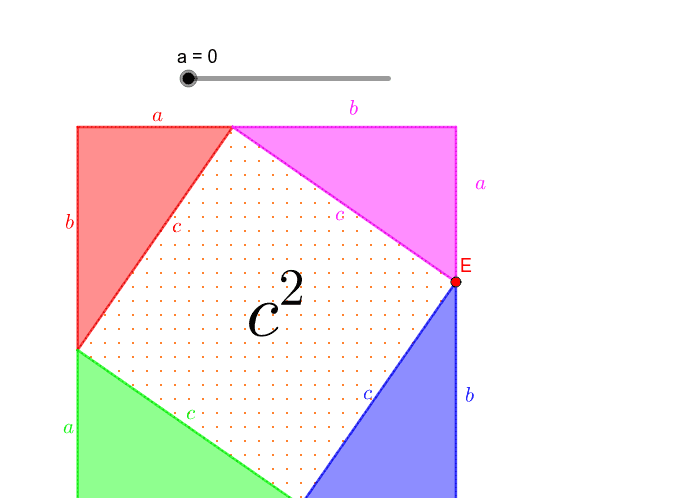



勾股定理证明2 Geogebra
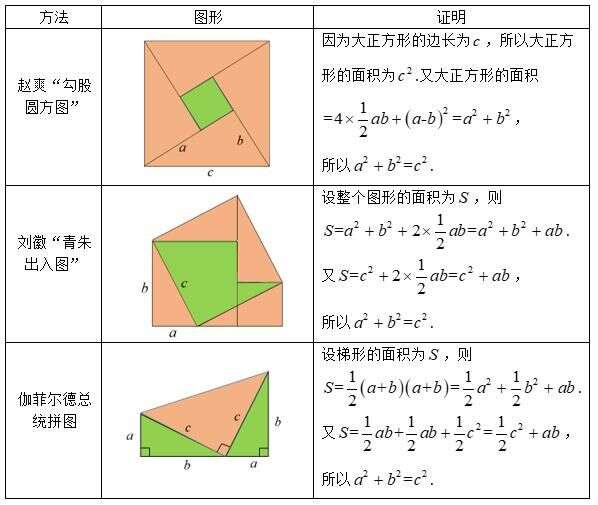



勾股定理及勾股定理的逆定理 楠木轩
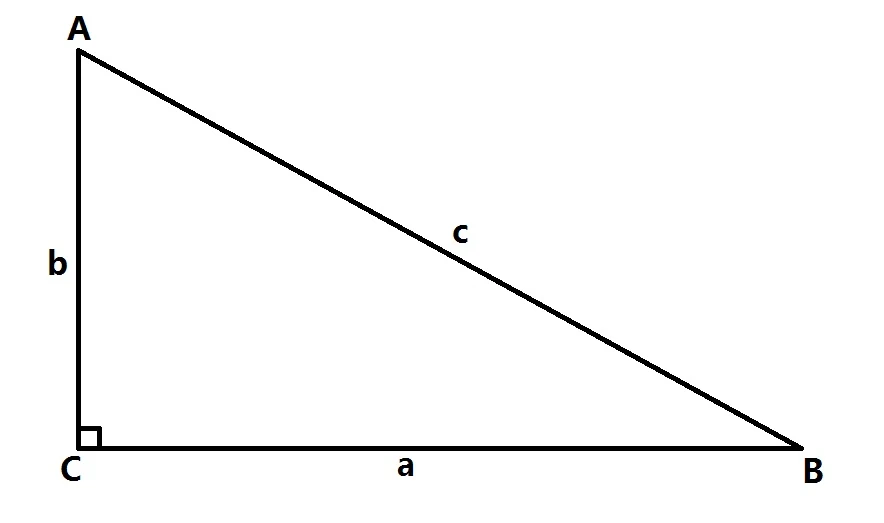
三平方の定理とは、直角三角形の3辺の長さの関係を表す公式の事を言います。 また、別名「ピタゴラスの定理」とも呼ばれています。 この呼び方の方が有名でしょうか。 古代中国でもこの定理は使われていて、それが日本に伝わり、江戸時代には鉤股弦初等幾何学におけるピタゴラスの定理(ピタゴラスのていり、英 Pythagorean theorem )は、直角三角形の3辺の長さの関係を表す。 斜辺の長さを c, 他の2辺の長さを a, b とすると、定理は = が成り立つという等式の形で述べられる 。 三平方の定理(さんへいほうのていり)、勾股弦の定理(こう 三角函數(英語: Trigonometric functions )是數學中常見的一類關於角度的函數。 三角函數將直角三角形的內角和它的兩個邊的比值相關聯,也可以等價地用與單位圓有關的各種線段的長度來定義。 三角函數在研究三角形和圓等幾何形狀的性質時有重要作用,也是研究振動、波、天體運動以



中考学霸坦言 吃透勾股定理这些题型 几何考试三角形从不丢分 基础知识



三角函数各边的关系图 图片欣赏中心 急不急图文 Jpjww Com
1、正弦定理 在一个三角形中,各边和它所对角的正弦的比相等,即在 abc中, (其中r为 abc外接圆的半径) 上式对任意三角形均成立 正弦定理可以变形为:① ;② , , ;③ , , ;④ , , 等形式,以解决不同的三角形问题 2、三角形中正弦定理的应用 全等三角形的判定定理 文/董玉莹 经过翻转、平移后,能够完全重合的两个三角形叫做全等三角形,而该两个三角形的三条边及三个角都对应相等。 判定定理 SSS(SideSideSide)(边边边):三边对应相等的三角形是全等三角形。このページでは,はじめに, sin ( α β) , cos ( α β) などの ( )をはずす公式 「三角関数の加法定理」 を解説し,その応用として 「2倍角公式」「3倍角公式」「積和の公式」「和積の公式」 を解説する. (1) (2)の証明・・・ (以下の証明は第1象限の




餘弦定理證明 信欣茗數學園地 隨意窩xuite日誌




三角勾股定理 勾股定理又叫畢達哥拉斯定理 商高定理和畢氏定理 在一個直角 百科知識中文網
上の正弦定理・余弦定理が必要なので、始めにそれらを導こう。 授業では、余弦定理の証明のみを行います。正弦定理についてはテ キストの最後に参考として証明を載せてあります。 単位球(=半径1の球)面上の三角形について次が成り立つ。高校数学Ⅰの「三角比」では、正弦定理と余弦定理がメインに出てきますよね。 でも、公式が多くて、全部覚えてたら頭がパンクしてしまいますよね。 三角比を攻略するには、sin cos tan の計算や正 フランクモーリーの定理の証明はいくつか知られていますが,まずはどの道具を使うか考えます。 一般に,図形の性質を証明する方法は大きく分けて3つあります: 初等幾何,図形的な性質のみで証明 三角関数を用いてゴリゴリ計算 座標またはベクトル
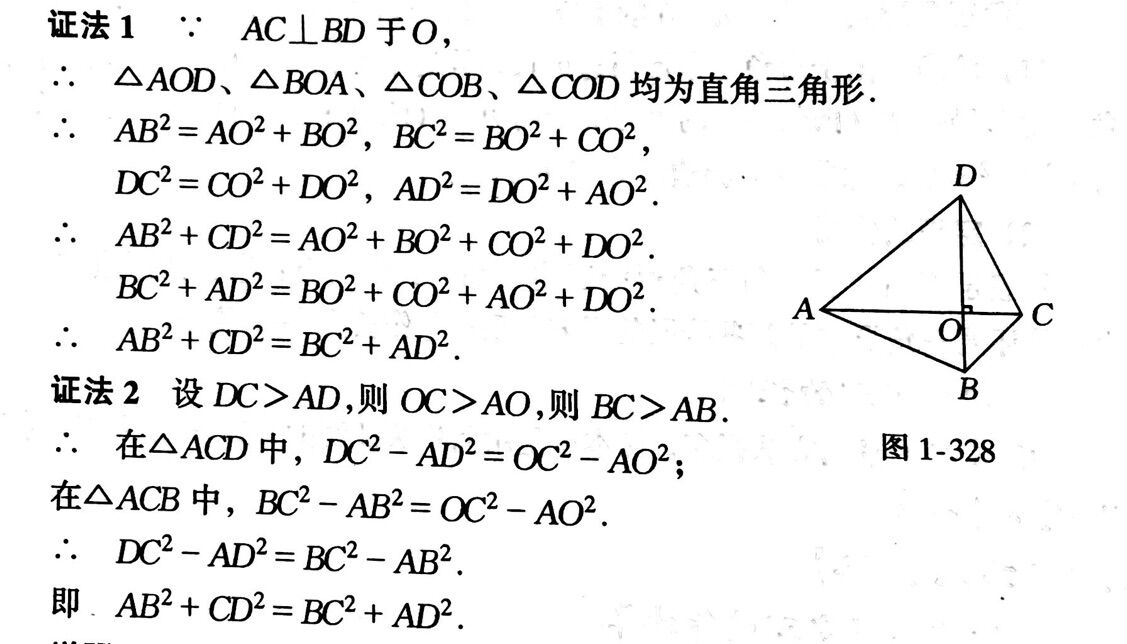



勾股定理及勾股定理的逆定理



教育还是严肃些好 希望少些为了博眼球而故意的浮夸 多些实在 腾讯新闻
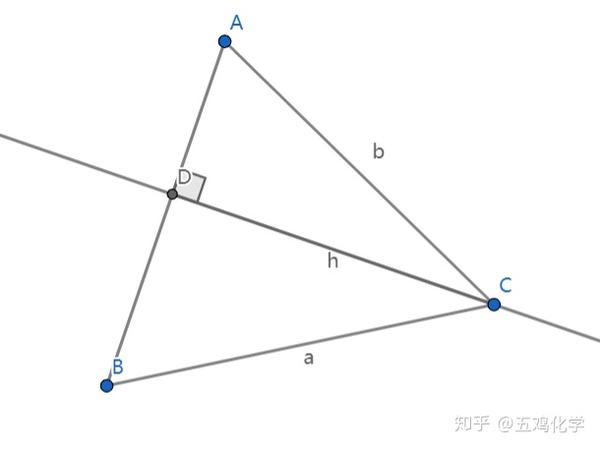
図形 定義・定理 まとめ 対頂角 𝟖は等しい 直線の角度 ° 平行線の 同位角 𝟖 は等しい 角形の内角の和 °×(𝒏− ) 平行線の 多角形の外角の和錯角 𝟔は等しい ° 同位角 が等しければ、2直線は平行 〇 合同な図形の対応する線分や角は等しこの図から,平面三角形a'bc'をぬきだす。(図3) また,この立体図を3つの扇形からできていると考え,半径ob で切り開いた展開図をかく。(図4) 球面三角形の定理 高校生に向けて 球面直角三角形abc におけるピタゴラスの定理 b c' a b c o a' α β γ α β γ 図4




狹義相對論中神奇的三角與勾股定理 每日頭條




你知道12歲的愛因斯坦是怎麼證明勾股定理的嗎 每日頭條




正弦定理 三角形正余弦定理 环球信息网



勾股定理的逆定理关于勾股定理的证明过程 学习岛




直角三角形斜邊中線定理 直角三角形斜邊中線定理是數學中關於直角三角形的一 百科知識中文網




2 2 5三角函數的基本概念 正弦定理與餘弦定理
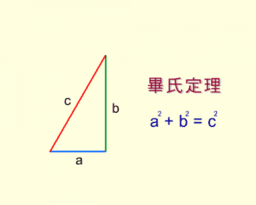



畢氏定理 勾股定理 Pythagorean Theorem Geogebra



1




如何使用勾股定理 12 步骤
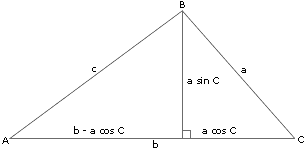



餘弦定理 维基百科 自由的百科全书



1




三角学 维基百科 自由的百科全书




高中数学三角函数公式大全及其易错题型总结 高中三角函数公式大全 天融网



几何中的ptolemy定理与两角和的三角函数 哔哩哔哩 つロ干杯 Bilibili



勾股定理 快懂百科



三角函数公式及其定理 图片信息欣赏 图客 Tukexw Com



直角三角形高度毕达哥拉斯定理 直角三角形png图片素材免费下载 图片编号 Png素材网
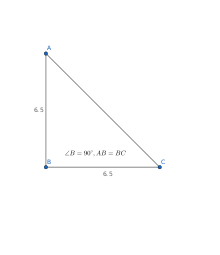



三角形 维基百科 自由的百科全书



怎样利用三角函数解决向量问题 勾股定理逆定理的应用



1 1 4 锐角三角函数与射影定理 人教版高中选修 B版 4 1数学电子课本 数九网




01 正弦定理解三角形高中数学 Youtube



三角函数定理公式大全 初三网



21版高考数学一轮复习第四章三角函数解三角形4 6正弦定理和余弦定理练习新人教b版 淘文库
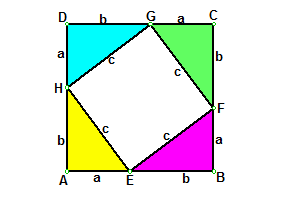



勾股定理的证明方法汇总一



三角定理讲课视频 西瓜视频搜索




餘弦定理 维基百科 自由的百科全书




相似三角形定理的证明




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




三角函数的正弦定理 三角函数正弦定理 三人行教育网 Www 3rxing Org



R Steriner定理的三角证法 科学猫



三角形勾股定理 如何学好三角函数和勾股定理 尚书坊



内弦图证明 万图壁纸网
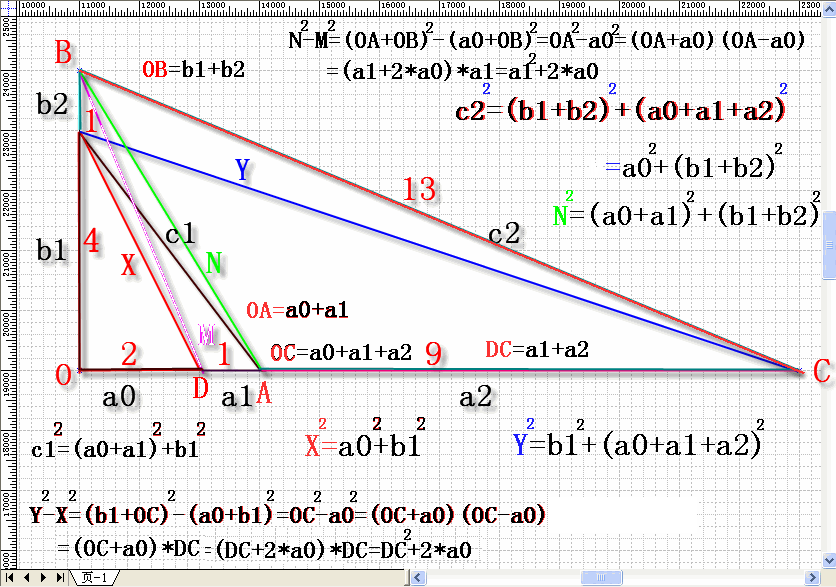



勾股定理为何能颠覆未来的 云世界 Hotpower的梦潭 与非博客 与非网



三角函数公式及其定理 三角函数 中考网
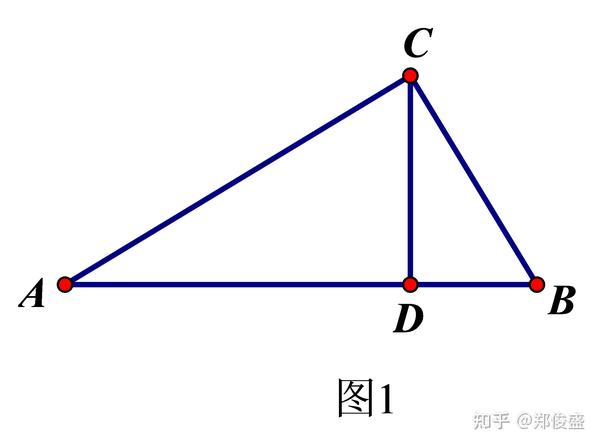



直角三角形射影定理逆定理 直角三角形的逆定理 射影定理逆定理成立吗
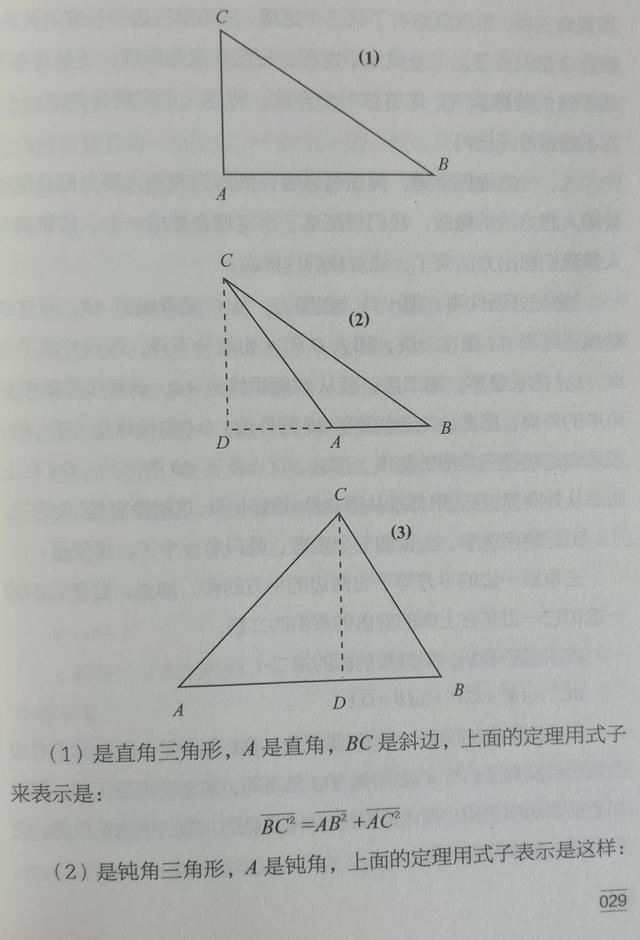



漫谈三角形三边关系定理



Q Tbn And9gcquu7lvijj0czribbb4t5dpi58u3hfjfhxdk8sbtanl1eauw2ct Usqp Cau



三角定理 简书



三角 反三角 函数在javascript中的应用 专注前端开发 十行笔记



由边的数量关系识别直角三角形 定理的应用 16 2由边的数量关系识别直角三角形 初中冀教版 数学中国网



三角函數的邊角關係 紀算 補習班 數學補習班 三重 文理補習班 數學公式 數學題庫 數學競賽 國小數學 國中數學 痞客邦




三角形中線定理 中線定義 性質 中線定理 定理證明 推論 中文百科全書




高三同学看过来 学好正余弦定理的应用 为三角系列划上完美




正弦与余弦定理 三角形与三角学 Mathigon




Ppt 勾股定理 畢氏定理 的證明powerpoint Presentation Free Download Id
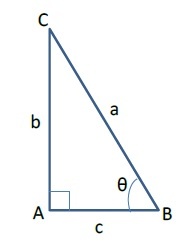



三角関数 の基本的な定理とその有用性を再確認してみませんか その1 正弦定理 余弦定理 正接定理 ニッセイ基礎研究所



三角函数 二 知乎




完整word版 正弦定理与余弦定理的证明 Doc 文档下载导航网



三角形的外角 三角形ppt下载 第一ppt




勾股定理 西安碑林区新曙光培训学校有限公司




畢氏定理x 圓x 三角學 余海峯david 物理喵phycat




勾股定理库存图片 图片包括有数学 分度器 笔记本 黑板 课程 知识 代数 白垩 几何




三角毕达哥拉斯定理正弦三角函数毕达哥拉斯三角恒等式 三角形png图片素材免费下载 图片编号 Png素材网




正弦定理 三角学中的基本定理 搜狗百科



余弦定理求三角形面积公式 高考辅导网
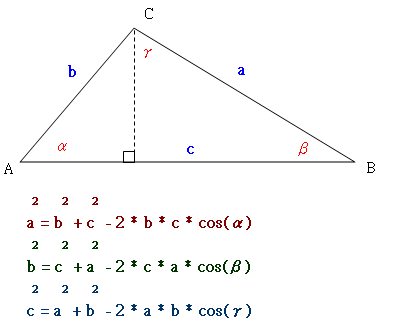



餘弦定理 Cosine Theorem Lexra Pixnet 痞客邦



勾股定理 锑星百科 Fandom




01利用勾股定理求边长勾股定理初中数学初二 Youtube




数学干货丨高中数学正弦定理的五种证明方法 学霸讲解 提分必备 3326学习网




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




正余弦定理 揭示三角形边角关系的定理 搜狗百科




觀念 三角形外角定理 數學 均一教育平台



少有人走的路 三角函数 正弦余弦定理及应用



全等三角形的性质定理 西瓜视频搜索



悟空问答 关于勾股定理 有哪些有趣的题目 7个回答



毕达哥拉斯定理库存例证 插画包括有
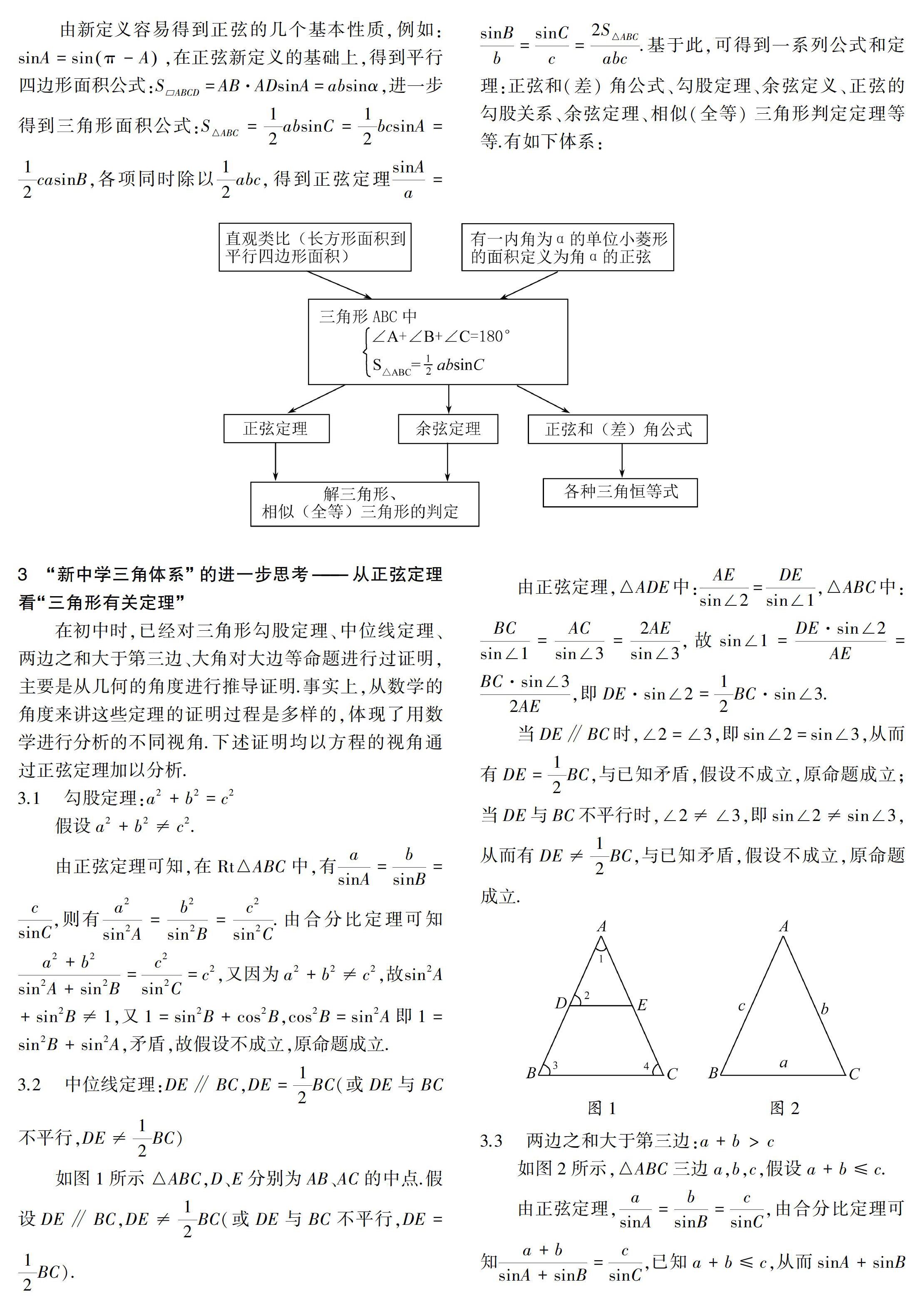



新中学三角体系 概述及其进一步思考 参考网




勾股定理的证明方法有多少种



三角马登定理椭圆复数三角形中的steiner点png图片素材免费下载 图片编号 Png素材网




三平方の定理 特別な直角三角形の3辺の比 中学生からの勉強質問 数学 進研ゼミ中学講座
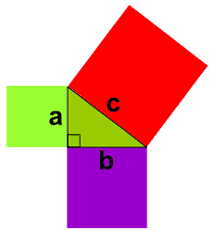



勾股定理




数学 三角形余弦定理证明 只布布倩 程序员宅基地 余弦定理 程序员宅基地



1




三角学 维基百科 自由的百科全书




五合一定理
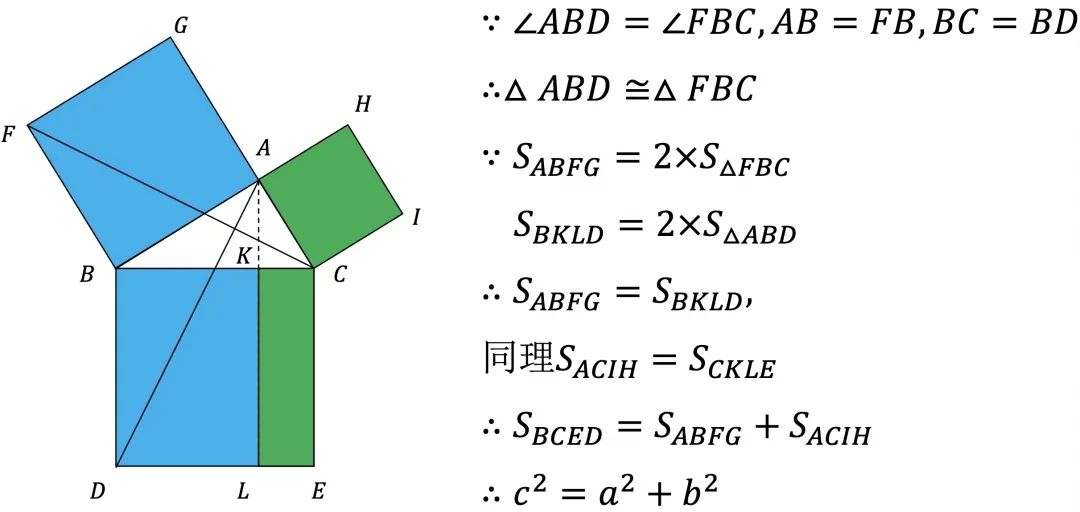



勾股定理竟然有500种证明方法 你会几种 小k算法 Csdn博客 勾股定理的500种证明方法




餘弦定理 维基百科 自由的百科全书




初二暑假数学勾股定理单元练习30题 附答案 人人焦点



三角函数定义 初中三角函数公式及其定理 尚书坊




三角関数 の基本的な定理とその有用性を再確認してみませんか その1 正弦定理 余弦定理 正接定理 ニッセイ基礎研究所




正弦定理 三角形正余弦定理 环球信息网
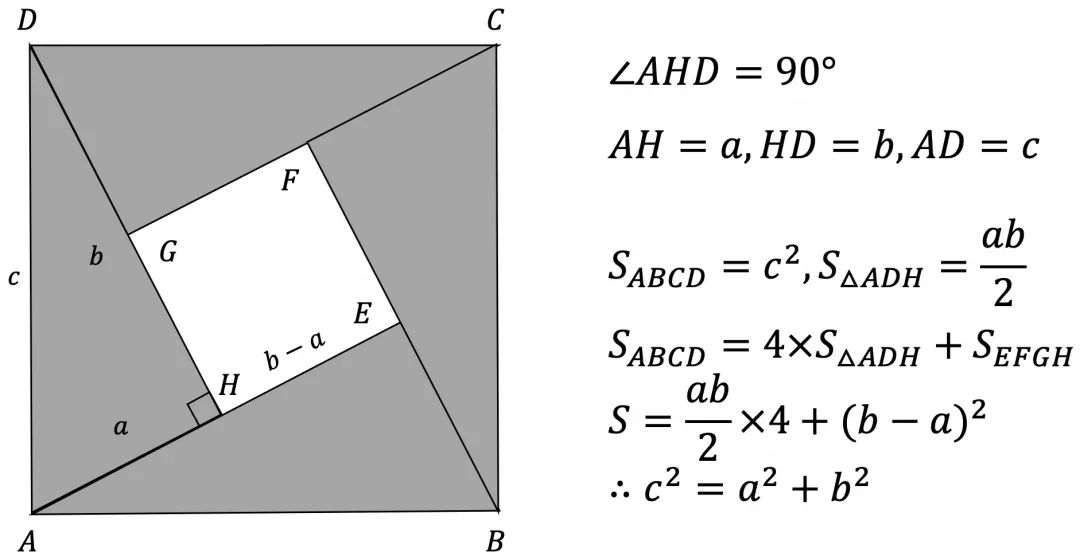



勾股定理竟然有500种证明方法 你会几种 小k算法 Csdn博客 勾股定理的500种证明方法



少有人走的路 三角函数 正弦余弦定理及应用




初中数学 勾股定理小课堂 精准命题 精准命题 大智教育 中小学课外辅导
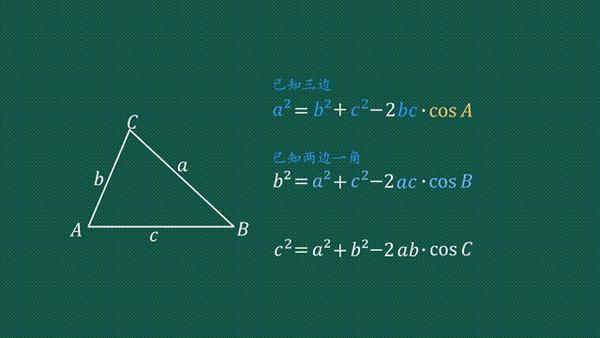



3分钟 搞懂余弦定理 知乎



利用证明勾股定理的 总统法 证明三角加法公式 科普之友




相似三角形判定定理 1 平行於三角形一邊的直線和其他兩 華人百科




高考数学考点之正 余弦定理及解三角形 王羽课堂




高考数学考点之正 余弦定理及解三角形 王羽课堂




三角形面积正切公式
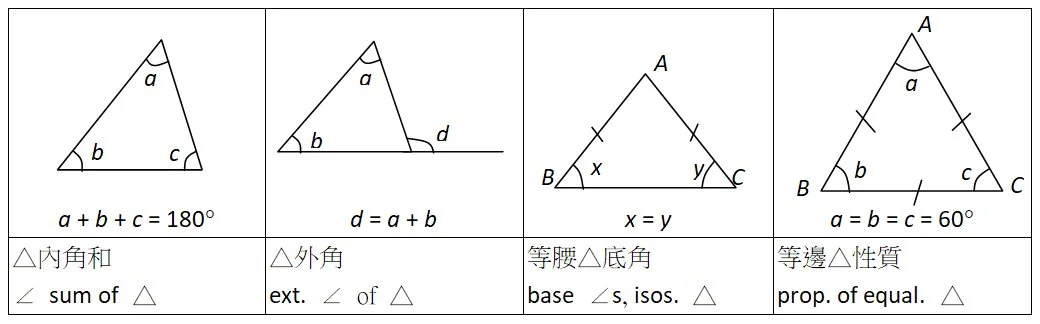



12 演繹推理幾何 與三角形有關的定理 齊齊溫




勾股定理應用2特殊直角三角形的勾股定理比例 Youtube



勾股定理公式计算 万图壁纸网




三角形相似与三角形的重心定理及衍生定理 正余弦定理 梅涅劳斯定理 哔哩哔哩



斜边中线定理如何证明直角三角形斜边中线定理 不要涉及高中知识 朵拉利品网
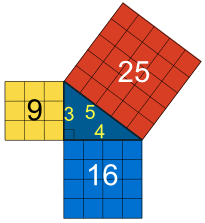



勾股定理



0 件のコメント:
コメントを投稿