三角形の3辺の長さから角度を求める 三角形の記号 使用する記号ですが、図のように、三辺の長さを\( a,b,c \)、角度を\(A,B,C\)で表すことにします。 角度は、次の2段階のステップで求めます。 求める角度の余弦(cos(コサイン))を求める。 基本的に、三角関数の角度は 半径 の「単位円」 を利用して求めることができます。 単位円 周分の角度は、度数なら 、ラジアンなら です。< 鈍角の三角比1 > 角度θが90 以上の場合の三角比を 次で定める。 正の数r に対し,点Q(r,0) を原点 O(0,0) を中心として反時計まわりに角 度θだけ回転した点をP(X,Y) とする。 このとき角度θにおける三角比を sinθ= Y r, cosθ= X r, tanθ= Y X で定める。

中学数学 正三角形の角度の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
三角形の角度の求め方
三角形の角度の求め方- 直角三角形の角度の求め方 こんにちは! 大神です。 今日は学校の 勉強は大事だよ ということを書いていこうと思います。 突然ですが皆さんは 「直角三角形の角度の求め方」 の公式を覚えていますでしょうか? サイン・コサイン・タンジェント3 三角形の種類(鋭角、直角、鈍角) 31 何三角形? 見極め方ポイント




二等辺三角形の頂角を求める問題の 逆 の問題 東大合格コム
(3)は右図のような場合で、作戦盤を書くと2つの角度が分かっていることになります。このような場合には高校で習う「正弦定理」や「余弦定理」以前の解き方があり、中学で習う三角形の内角の和の公式 abc=180 ° a=180 ° −b−c直角三角形の角度の出し方を教えてください!! 直角三角形で、3辺の長さがわかっている場合に残り2つの角度の出し方を教えてください!!①電卓がある場合(関数機能のないもの。ルート機能だけある Read 523 直角三角形の角度の求め方 教えて下さい。三角形の合同条件を使って、合同な三角形を見つける方法! 証明の書き方合同な三角形の証明問題の書き方を基礎から解説! 直角三角形証明問題の書き方とは?合同条件の使い方を徹底解説! 二等辺三角形の角度の求め方 厳選6問解説!
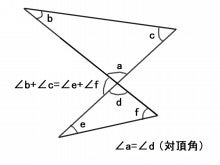
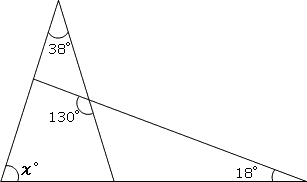
三角形の外角の大きさ=となり合わない2つの内角の和 であることから x+60°=135° x=135°-60°=75° (1)三角形の内角の和と外角の定理を利用して、三角形の角の大きさを求めましょう。まず、内角と外角とは何か学んでいきましょう。 三角形の内角の和は、全ての 多角形 たかっけい の角度を求めるときの基礎です。 下の四角形のaの角度を求めなさい。 解説 下の図のように四角形の1本の対角線で2つの三角形に分けます。 三角形の内角の和は180°なので、この四角形の内角の和は180°×2=360°になります。 ですのでaの角度は、360°(72°38°30°)=2° よって、 答え a=2 °
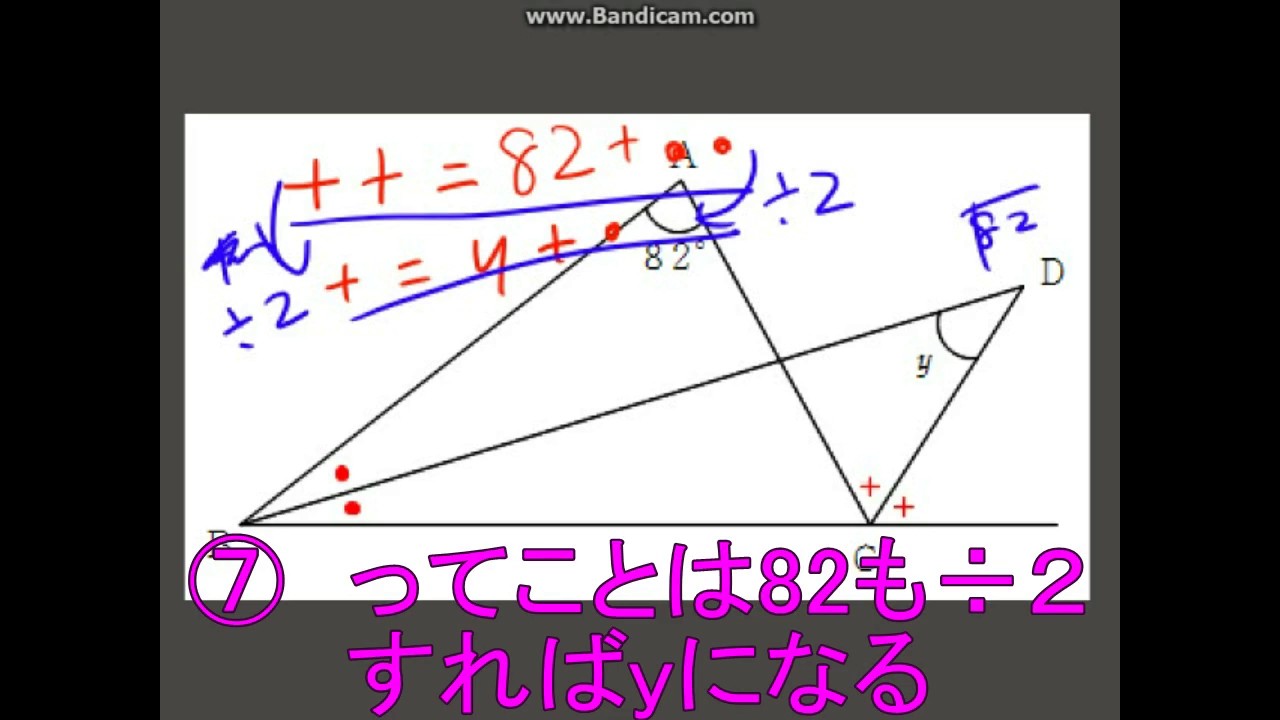
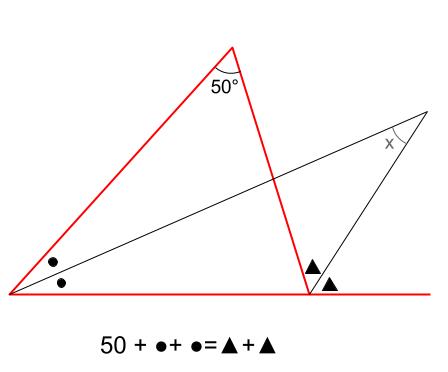
二つの特別な直角三角形の角度と辺の長さの比の関係を暗記しよう! 「サイト内お気に入り」に登録する 数多の直角三角形のうち、二つの特別な直角三角形の三つの辺「底辺」「高さ」「斜辺」の長さの比の関係は簡単な数字で表される。 二つの特別な 三角形の内角と外角の関係から ● = ○ + ● 角A=30°+90°=1°三角関数の角度を計算する場合、「エクセル」を使うと便利です。 θ=Arcsin (038)のような半端な辺の比に対する角度も計算できます。 まずエクセルのセルに「= ASIN (038)」と入力してください。




数学 中2 53 角度チャレンジ Lv 1 Youtube



2 偶然の角 の一般化にむけて 二等辺三角形から一般の三角形に
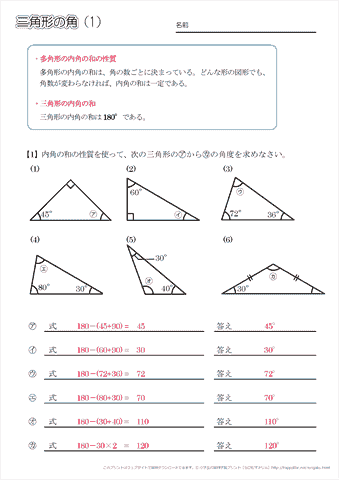
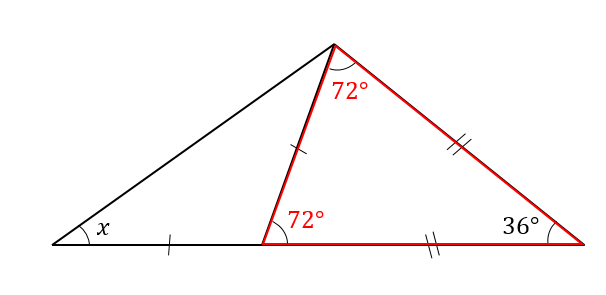
答え 二等辺三角形が2つくっついている問題ですね。 この場合、それぞれの二等辺三角形に注目して角度を1つずつ求めていきます。 赤い二等辺三角形は、頂角が36°なので 底角1つ分の角は となります。 そこから、次は青い二等辺三角形に注目して を Contents 1 三角形の内角 11 問題;小学校5年生で習う「三角形の内角の角度」 を求める問題集です。 問題をランダムで生成することができ、答えの表示・非表示も切り替えられます。印刷してご活用ください。 ちなみに三角形の内角の角度の求め方についてはこちらに詳しく説明しています。




三角形の角度を求める問題 小学生 中学生の勉強
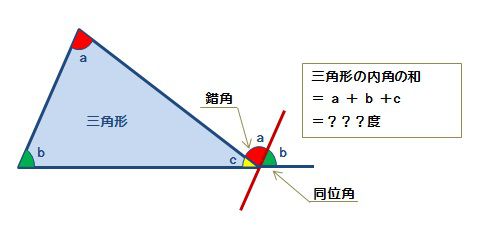



三角形の内角の和 算数の公式覚えてますか
三角形の「2辺の長さの比」が正弦の値になるのは直角三角形の場合だけで、それ以外の場合には sin A の値は「2辺の長さの比」にはなりません。 (右図イのような場合も含めて)一般に、角度 A の値によって sin A の値が決まり、これとは別に辺の長さが決められていると考えることが重要です。計算例 答えの度分秒(° ′ ″ )は、秒の小数点以下2桁まで求めています。 \) お客様の声 アンケート投稿 よくある質問 リンク方法 底辺と高さから角度と斜辺を計算 三角形の3辺から角度を まず正五角形は三角形3つの集まりで表せるので、内角の和は180×3で540°。 内角は5つなので540÷5=108(°)となる。 正五角形の内角は108° するとここを頂角にした二等辺三角形が見えてきたと思うので、底角を出す。さっそく二等辺三角形が出てきてうれしい。



円と三角形 角度 中学から数学だいすき
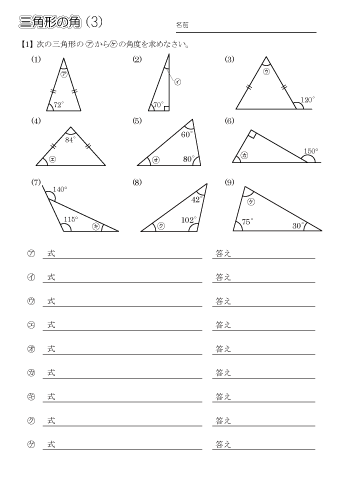



小学5年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生
三角形の角度 無料で使える中学学習プリント 三角関数の基礎角度の求め方とは? (sinθ=1/2からθを計算 三角形の面積の求め方まとめ。 タイプ別でわかる公式一覧 三角形の面積は「 \ (底辺×高さ÷2\) 」という公式から求まりますが、この公式以外三角形にはいろんな種類があり、形や大きさは様々です。しかしどんな三角形でも、 「\(3\)つの角の内角をすべて足すと絶対に\(180°\)になる」 という定理があります。 「図の\(a\)の角度を求めよ」というような問題が出された場合にこれを用います。・直角三角形(高さと角度) 直角三角形の高さと角度から、底辺と斜辺と面積を計算します。 ・直角三角形(斜辺と角度) 直角三角形の斜辺と角度から、底辺と高さと面積を計算します。 三角関数




円の中にある二つある三角形の角度の求め方 Okwave




三角形面積求め方 三角形とは 面積公式 角度 辺の長さ 重心 比の計 Jbqhd
三角形における三角比の値 ABCでcosB の値を求めよ。 という問題で,cosB =3/2 と答えてしまいました。 sinθ ,cosθ ,tanθ の定義通りにあてはめたつもりですが,答えが正しくありませんでした。次に㋑を求めてみます。 右の図で三角形fpdに着目すると、三角形の内角の和は180°だから、 180°-(70°+90°)=° で、角fpdは°です。 さらにpに着目して、直線の角は180°であることより ㋑+90°+° =180°だから ㋑=70° となります。≪三角比の値の求め方≫ sinθ,cosθ,tanθの値は,次の「よく出る2つの三角形」と「sinθ,cosθ,tanθの定義」を覚えていれば導けます。 これらを使った求め方 ①θの値(角度)を見て,「よく出る2つの三角形」のうち,当てはまる三角形をかき出す。




正弦定理から 三角形の辺の長さを求める計算について 数学 苦手解決q A 進研ゼミ高校講座




二等辺三角形の頂角を求める問題の 逆 の問題 東大合格コム
まずは、角度Bは簡単に求まります。三角形の内角の和は180度ですから、「C = 180 A B = 180 35 90 = 55」より、角Cの大きさは55度だと分かります。 aとbの求め方 次に、aとbを求めてみま求角と方程式 角度を求めることは、小学生のころにもやっていることです。 しかし、角度を求めるために方程式を用いることは中学生ならではです。 そんな問題を練習しましょう。 例題1 次の図の角 \(x\) の大きさを求めなさ2 三角形の外角 21 三角形の1つの外角は、その隣にない2つの内角の和と等しい;




三角形の辺や角が与えられたとき残りの辺や角を求める方法 数学の偏差値を上げて合格を目指す




三角関数 機械加工でよく使う計算方法を説明します セドヤのブログ
すると三角形が2つできます。 この三角形は単位円が半径1であることと、交点のy座標が であることから辺の比を求めることができます。 今回できた三角形は の三角形であるため、30°、60°,90°の三角形であることがわかりますね。三角形の面積は「 \(底辺×高さ÷2\) 」という公式から求まりますが、この公式以外にも色々な方法で三角形の面積を求めることができます。 このページでは、そんな三角形の面積の求め方をタイプ別に見ていきましょう。
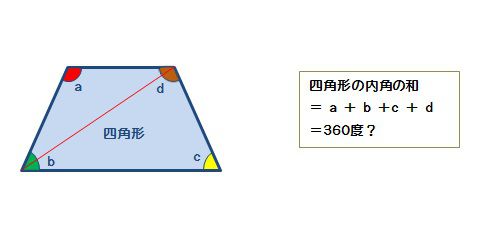



四角形の内角の和 算数の公式覚えてますか
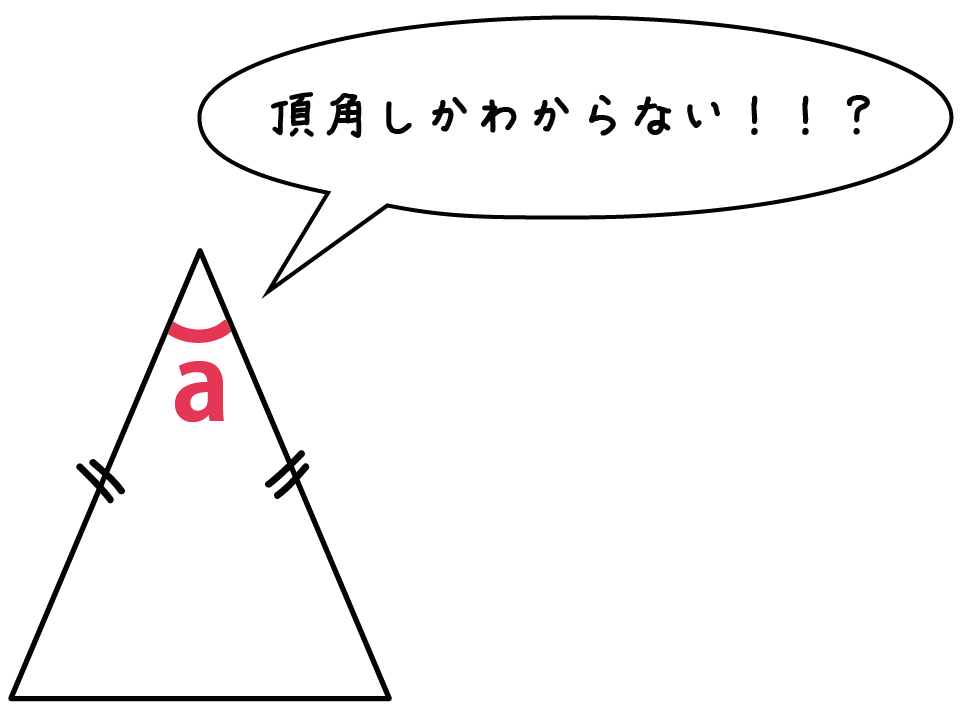



簡単公式 二等辺三角形の角度の2つの求め方 Qikeru 学びを楽しくわかりやすく




中学数学 正三角形の角度の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




二等辺三角形を使う角度計算です 一応解けたのですがもっと簡単な式があると思うので教え Clear




角度の問題まとめ 無料で使える中学学習プリント




底辺と高さから角度と斜辺を計算 高精度計算サイト



角度の求め方 数学が嫌いなんです




角度の求め方 角度の求め方 Mqttk




二等辺三角形の定義 角度の性質を使った証明問題などを解説 遊ぶ数学




三角形の辺から角度を計算 製品設計知識



ラングレーの問題 整角四角形




中2数学 二等辺三角形の3大重要ポイント 映像授業のtry It トライイット
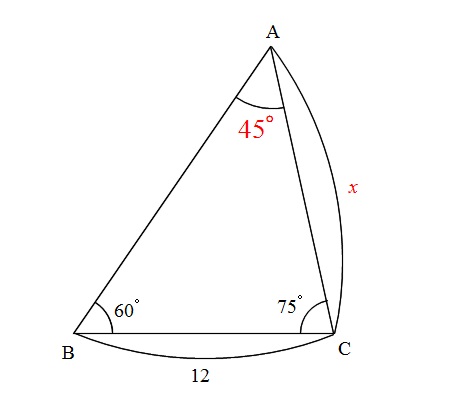



三角形で角度が2つ分かっているのに正弦定理も余弦定理も使えない
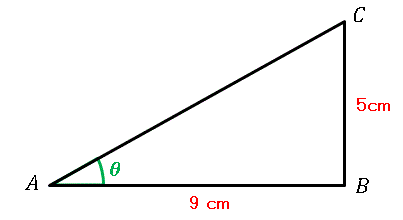



Excel で直角三角形の斜辺と底辺に挟まれた角度を求めます
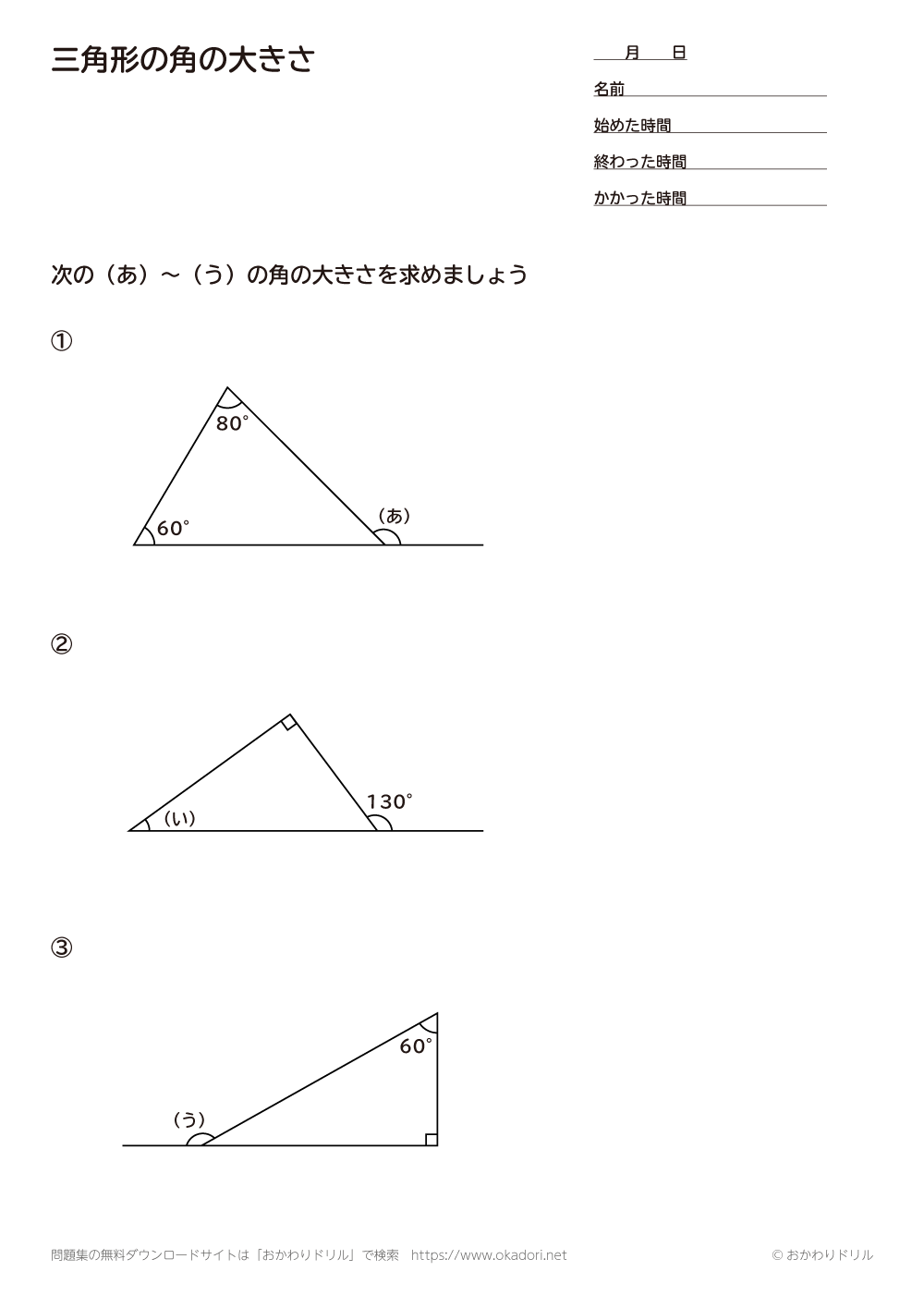



小学5年生 算数 無料問題集 三角形の角の大きさ おかわりドリル




三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ



角度の求め方 算数の教え上手 学びの場 Com



小学5年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生



3




角度を計算する方法 9 ステップ 画像あり Wikihow




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集
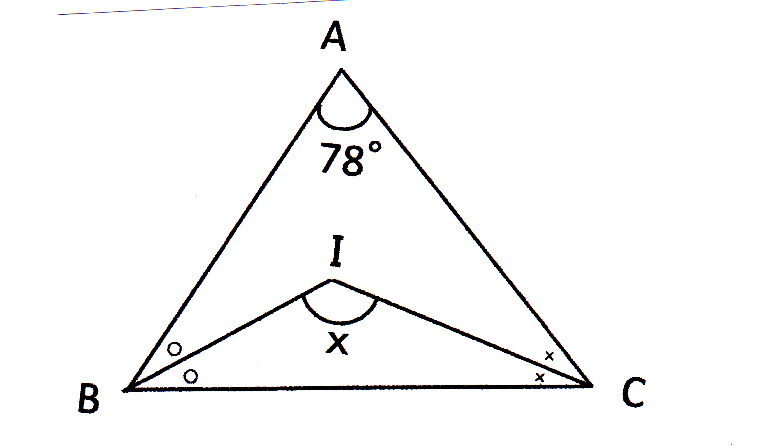



三角形内の角度を求める問題 現役塾講師のわかりやすい中学数学の解き方




直角三角形の角度の求めかたは 直角三角形の残りの角度を求める 数学 教えて Goo




高校数学 三角形の辺と角の関係 映像授業のtry It トライイット
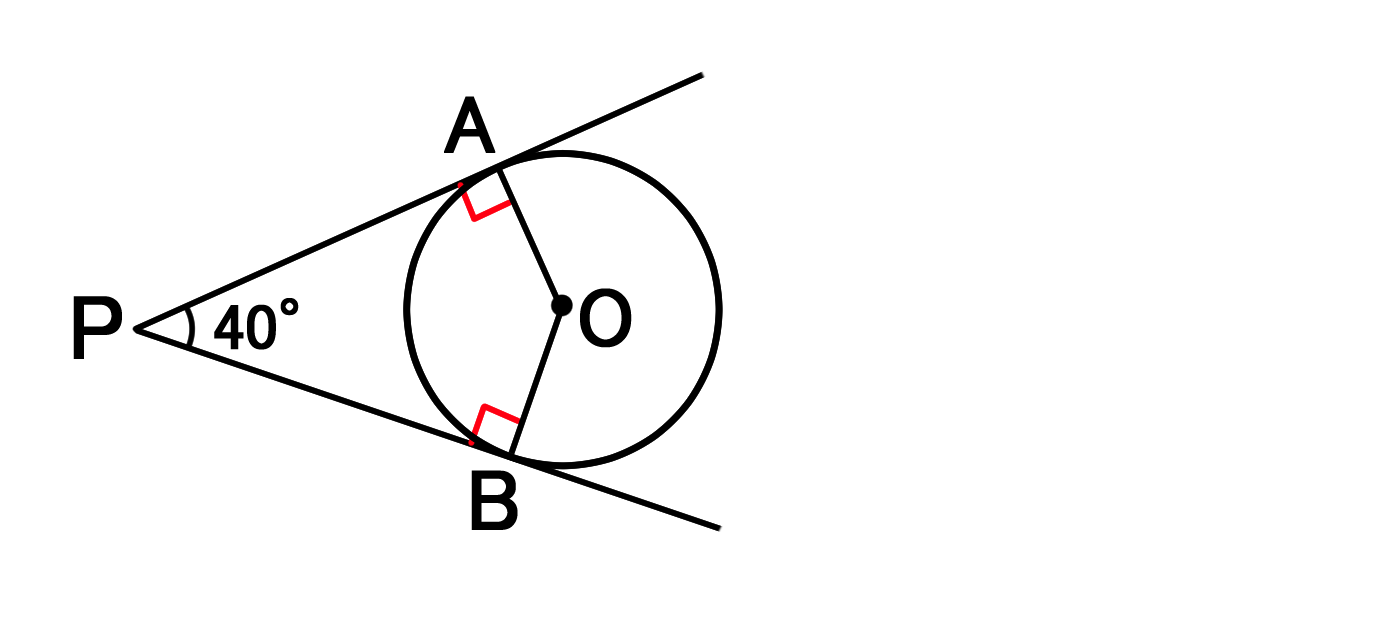



円と接線の性質を利用して図形の角度を求める問題 バカでもわかる 中学数学




内心とは 三角形の内心の求め方や比の使い方 性質の証明 位置ベクトルをわかりやすく解説 遊ぶ数学




小学5年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生




正三角形や二等辺三角形の内角 Youtube



中学二年 数学 三角形の角度の求め方 中の上編 Youtube




あ かまでの角度を求めてください 急いでます 教えてください Clear



二等辺三角形の角度は 1分でわかる求め方 計算 辺の長さとの関係 証明




算数の問題でもあり 数学の問題でもありますの解答解説1 角度を求める問題7月19日出題 Fitのひろば




中2 数学 4 2 三角形の角度の利用 Youtube
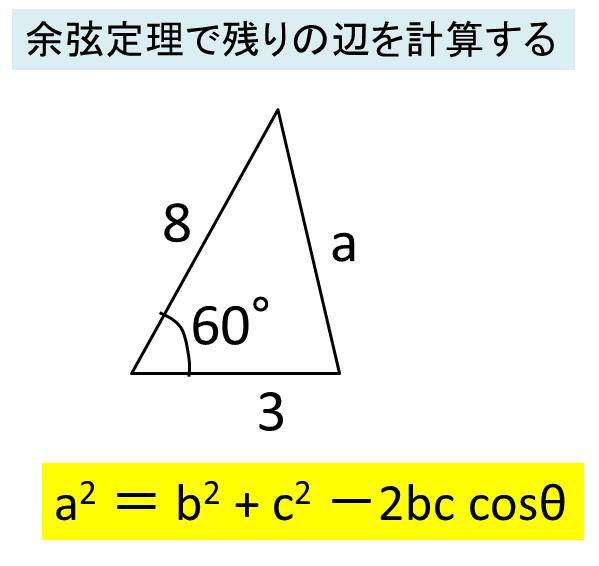



Excel エクセルで余弦定理の計算をする方法 角度や辺の長さを求める
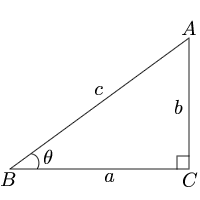



三角関数から角度 逆三角関数 三角形の計算 計算サイト




二等辺三角形の角を求める Youtube



Kids Gakken Co Jp Box Sansu 05 Pdf B Pdf



直角三角形の解法 1



普通の電卓で計算できる直角三角形の近似計算




余弦定理とは何か 図解でわかるその使い道と公式の証明 アタリマエ
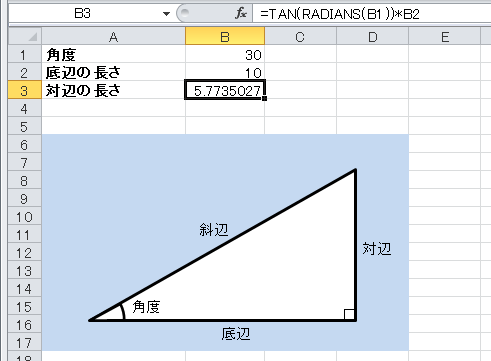



角度からタンジェントを計算するには Tan Radiansの解説 エクセル関数リファレンス
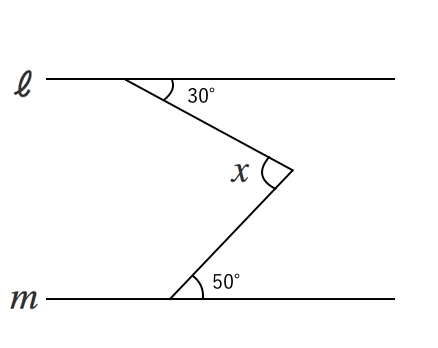



図形の調べ方 三角形 役に立つ角度の求め方 苦手な数学を簡単に



三角関数 1 Cg 数学 06aa




高校数学 三角比からの角度の求め方2 Cos8 例題編 映像授業のtry It トライイット
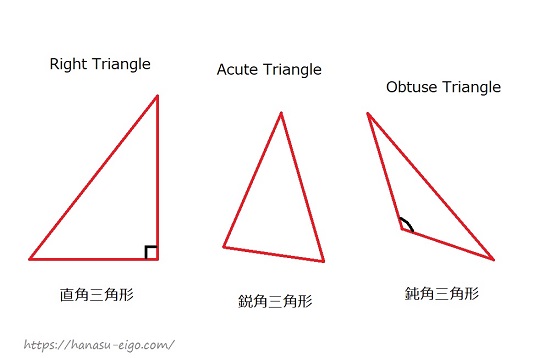



三角形 を英語で説明しよう 正三角形は 二等辺三角形は 話す英語 暮らす英語



3



紙ヒコーキ型図形の角度を求める 平行線と角 勉強ナビゲーター
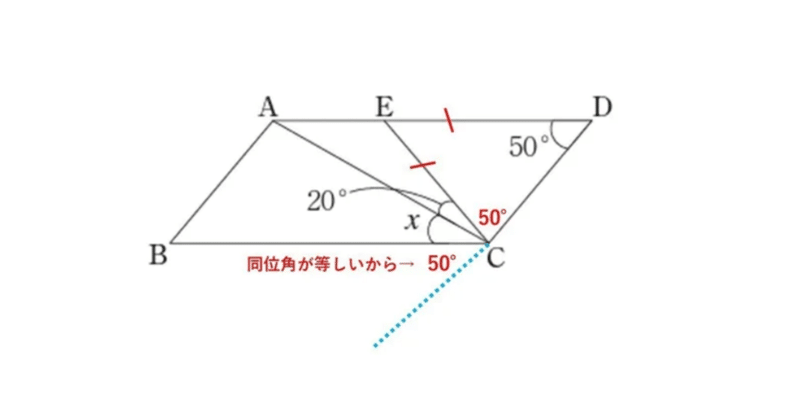



中学数学の平面図形の角度を求める問題を通して学び直しする論理 数学の基礎 タロウ岩井の数学と英語 Note
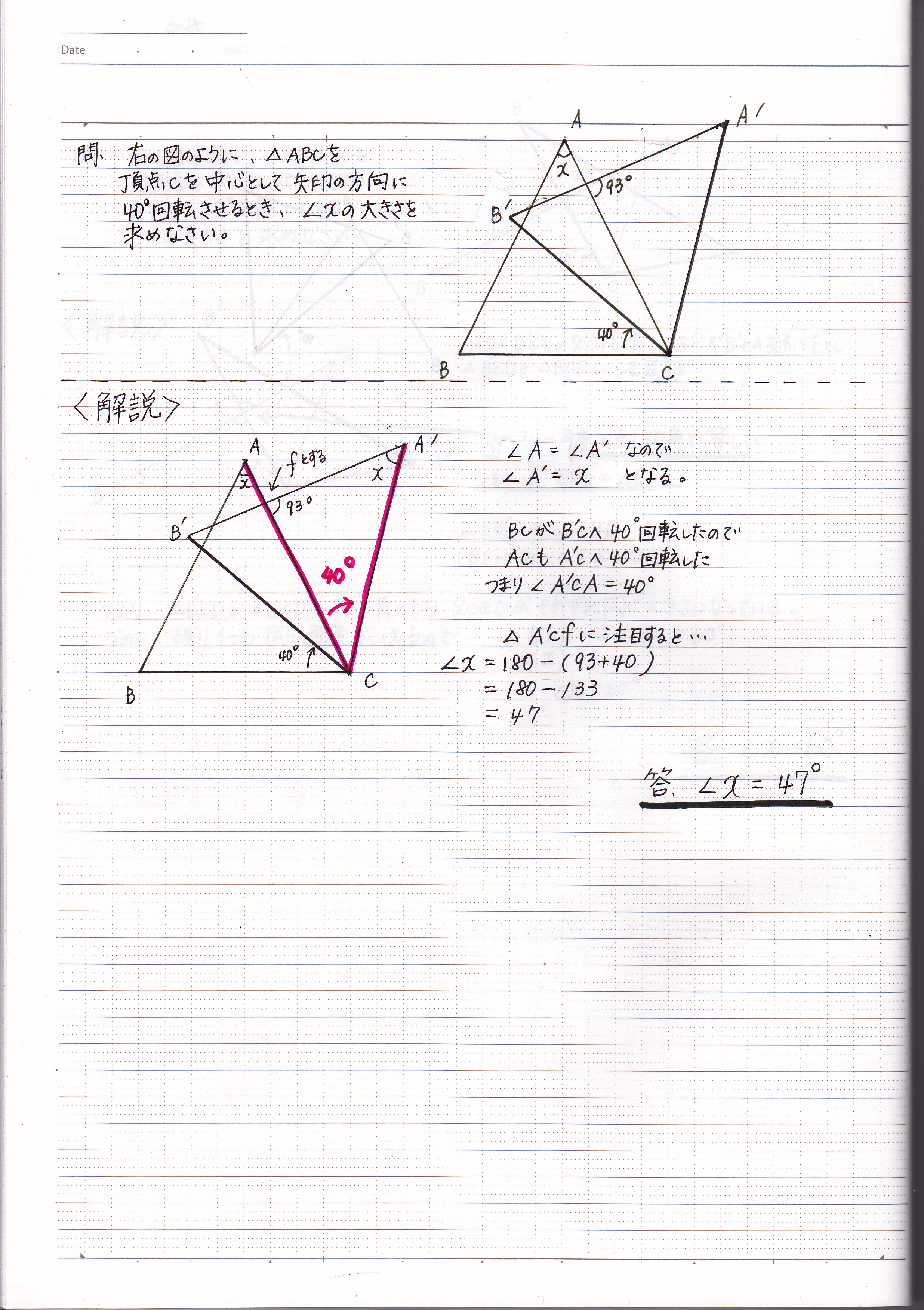



回転する図形の角度の求め方 現役塾講師のわかりやすい中学数学の解き方



正三角形とは 定義や面積公式 高さや角度の求め方 受験辞典
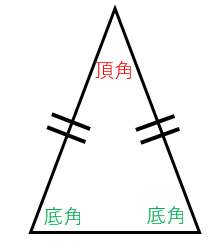



二等辺三角形の角度の求め方と例題 具体例で学ぶ数学



直角三角形の角度の求め方 教えて下さい 斜辺以外の2辺の長さが分かっ Yahoo 知恵袋
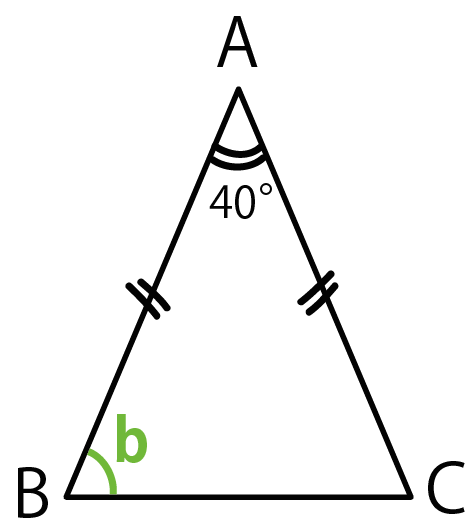



簡単公式 二等辺三角形の角度の2つの求め方 Qikeru 学びを楽しくわかりやすく




円の中に三角形角度の求め方 いろんな角度の三角関數を単位円で考える Qmog Fi




接弦定理とは何か 角度別に分かるその証明方法 アタリマエ




図形の調べ方 三角形 役に立つ角度の求め方 苦手な数学を簡単に
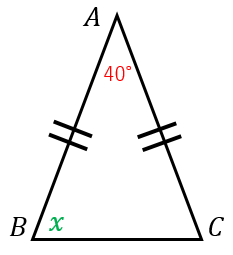



二等辺三角形の角度の求め方と例題 具体例で学ぶ数学




中2数学 ブーメラン型角度の求め方を解説 数スタ




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ




数学 角の二等分線にまつわる絶対に覚えておきたい公式 受験の秒殺テク 8 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



1




角度の求め方 算数の教え上手 学びの場 Com
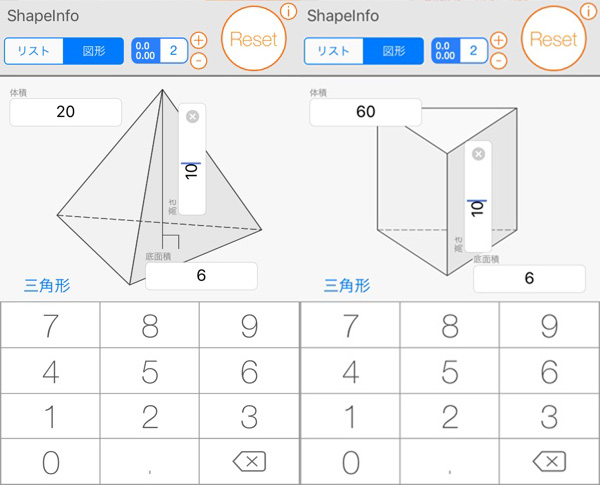



三角形や球も 様々な図形の面積や角度がすぐに分かる 図形電卓 が超便利 Isuta イスタ 私の 好き にウソをつかない




三角形の角度を求める問題 小学生 中学生の勉強



中学数学 求角と方程式 中学数学の無料オンライン学習サイトchu Su



二等辺三角形の角度の求め方を問題を使って徹底解説 数スタ




三角形の3辺から角度を計算 高精度計算サイト




黄金三角形による18 シリーズの三角比 おいしい数学
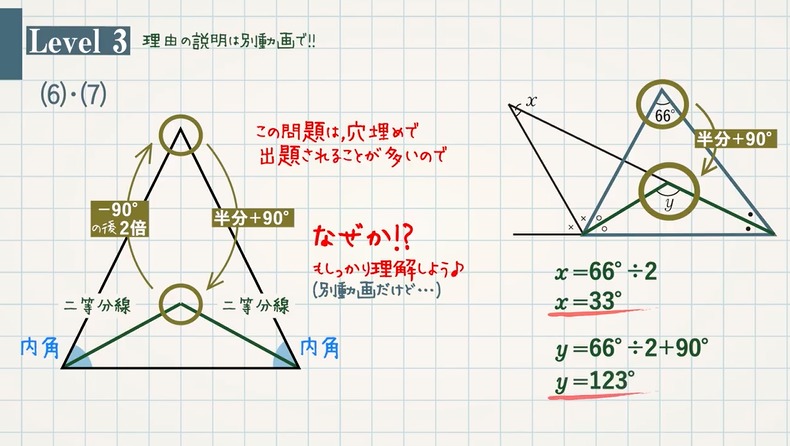



角度の計算 裏技まとめ 教遊者



1




角度の求め方 算数の教え上手 学びの場 Com




外角の求め方 外角の和を使って多角形の角度を求める問題 中学や高校の数学の計算問題




小学4年生 角度の求め方は 対頂角 平行線 同位角 錯角 中学受験 そうちゃ式 受験算数 2号館 図形 速さ




二等辺三角形の角度の問題 基礎から応用までパターン別に解説 中学数学 理科の学習まとめサイト




小4算数の角度の問題 折り返し 錯角 同位角で混乱する
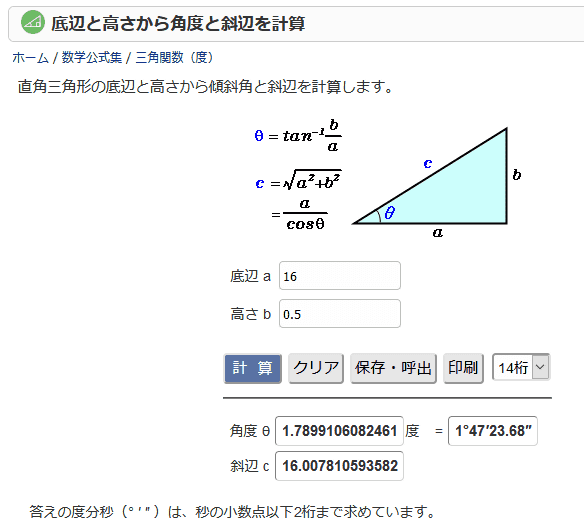



表計算ソフトを使って 底辺 と 高さ から 角度 を求める
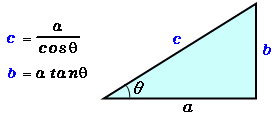



角度と底辺から斜辺と高さを計算 高精度計算サイト



三角形の角度を求める 思考力を鍛える数学




ブーメラン型四角形 凹四角形 の角度を求める方法 Qikeru 学びを楽しくわかりやすく




直角三角形公式角度 直角三角形 斜辺と角度 三角形の計算 計算サイト翻譯此網頁 Rzcpe




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ
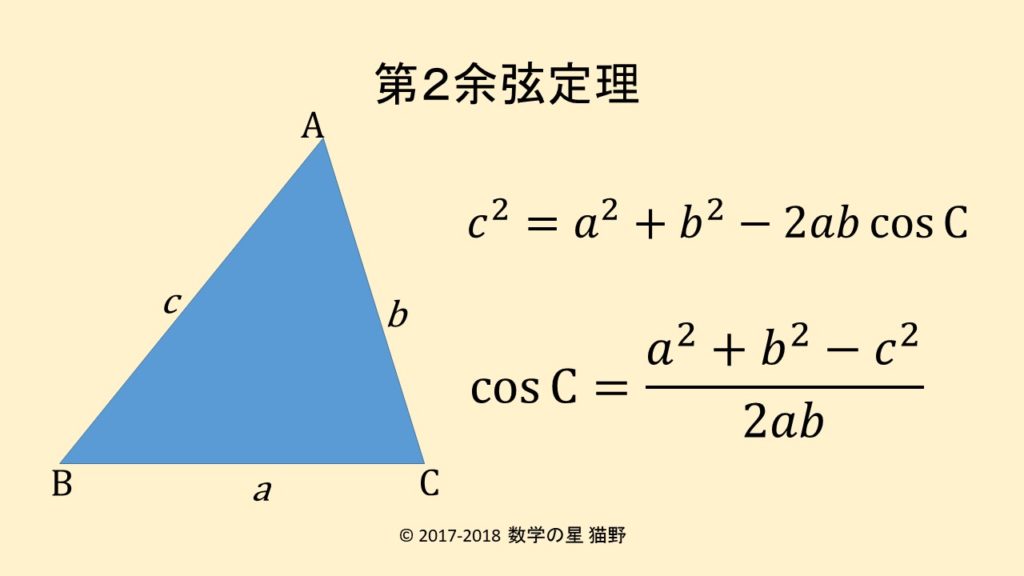



第2余弦定理の公式は辺と角度の関係を簡潔に表す 数学の星




中高生必読 知らないとヤバい二等辺三角形の知識 定義 角度 面積 高校生向け受験応援メディア 受験のミカタ




小5 算数 小5 31 三角形の角 Youtube
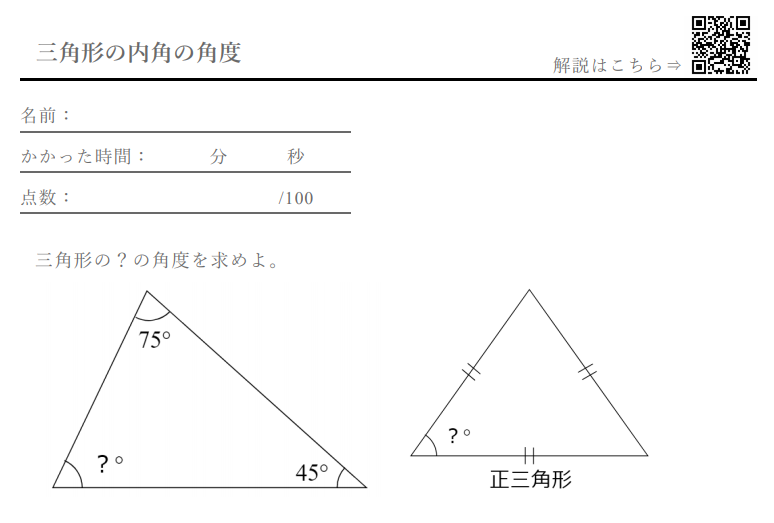



三角形 の内角の角度 計算ドリル 問題集 数学fun




Xの角度の求め方を教えて下さい Clear




タンジェントとは何か 中学生でも分かる三角関数の基礎




Excel 三角形の角度を底辺や斜辺 高さから求める方法 直角三角形の角度の計算



直角三角形とは 定義や定理 辺の長さの比 合同条件 受験辞典




高校数学 直角三角形を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 30 45 60 の三角比 受験の月




余弦定理で角度を求める方法 数学の星
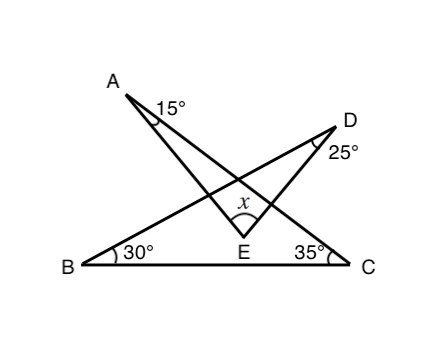



角度を求める問題 スリッパを探そう 苦手な数学を簡単に



0 件のコメント:
コメントを投稿