++ 50 ++ 5−2√3 7 4√3 = a − b√3 find the value of a and b 261200

The surds are 7√2, 5√3, 4√7, 2√5 Concept used If a 2 > b 2, then a > b Calculation (7√2) 2 = 98 (5√3) 2 = 75 (4√7) 2 = 112 (2√5) 2 = Here, 112 > 98 > 75 > ⇒ 4√7 > 7√2 > 5√3 > 2√5 ∴ The correct order is 4√7 > 7√2 > 5√3 > 2√5 Download Question With Solution PDF ››Solve for b 3/2b=7/4 3 2 b = 7 4 3 2 b = 7 4 Subtract 3 2 3 2 from both sides of the equation b = 7 4 − 3 2 b = 7 4 3 2 Simplify the right side of the equation Tap for more steps To write 3 2 3 2 as a fraction with a common denominator, multiply by 2 2 2 2 b = 7 4 − 3 2 ⋅ 2 2 b = 7 4 3 2 ⋅ 2 2Simplify i 3√2−2√33√22√3√12√3−√2ii 73√53√5−7−3√53−√5 i 3√2−2√33√22√3√12√3−√2Now 3√2−2√33√22√3=3√2

Curve Fitting And Solution Of Equation

5−2√3 7 4√3 = a − b√3 find the value of a and b

5−2√3 7 4√3 = a − b√3 find the value of a and b-7 x − 4 = 7 x 3 5 x 4 Multiply both sides of the equation by 35, the least common multiple of 7,5 Multiply both sides of the equation by 3 5 , the least common multiple of 7 , 5The problem, math (√2√3)^2/math math=(√2)^2(√3)^22(√2*√3)/math math=232√6/math math=52√6/math Now, math 2√6=√24=4

Wolfram Alpha Examples Step By Step Solutions

 Rationalising denominator of irrational number Add (3√27√3) and (√2−5√3) Divide 5√11 by 3√33√ b ,Q √ a2 −b and Q √ b √ a2 −4b The irreducibility of the polynomial implies that √ a2 −4b is not rational Therefore if √ b, √ a2 −4b √ b /∈ Q, the splitting field contains at least at least three subfields of degree 2 Hence the Galois group is either K4 or D4 However, ifThis problem has been solved

=√(7√(4 X 4 X 3)) this is in model (ab) square = a square b square2ab =√(342√4√3) =√(√3√4)(√3√4) =√3√4 Hence Answer=√32Question (View in Hindi) If 35a 7√15 = 28, then find the value of (2√a 2/√a) Free Practice With Testbook Mock TestsSteps Using Factoring By Grouping 6 { x }^ { 2 } 13x5 = 0 6 x 2 1 3 x − 5 = 0 To solve the equation, factor the left hand side by grouping First, left hand side needs to be rewritten as 6x^ {2}axbx5 To find a and b, set up a system to be solved To solve the equation, factor the left hand side by grouping

Solutions for Chapter 93 Problem 6E Find a ba = 6, −2, 3 , b = 2, 5, −1 Get solutions Get solutions Get solutions done loading Looking for the textbook?A 3 B 4 C 5 D 7 Answer Option B Solution ( ) ( ) ( ) ( ) = 2 A 3 − B 3 = (A − B) (A 3 AB B 3) A 2 − B 2 = (A B) (A − B) ⇒ √ √ ⇒ √ √ = √ ⇒ x = −1 16 = 3, then the value of m is?A 5 √5 B 253 √C 35 D 5√3 12 Simplify (2 3)2(5 4)?

Rationalize The Denominator And Simplify I 3 2 3 2 Ii 5 2 3 7 4 3 Sarthaks Econnect Largest Online Education Community

The Coordinates Of The Vertices Of A Rectangle Are 3 5 0 4 3 7 And 6 2 How Do You Find The Area Of This Figure Socratic

11 Which expression is equivalent to √75 ?Click here👆to get an answer to your question ️ If 5 2√(3)/7 4√(3) = a b√(3) , then the value of a and b Rationalising denominator of irrational number Add (3√27√3) and (√2−5√3) Divide 5√11 by 3√33

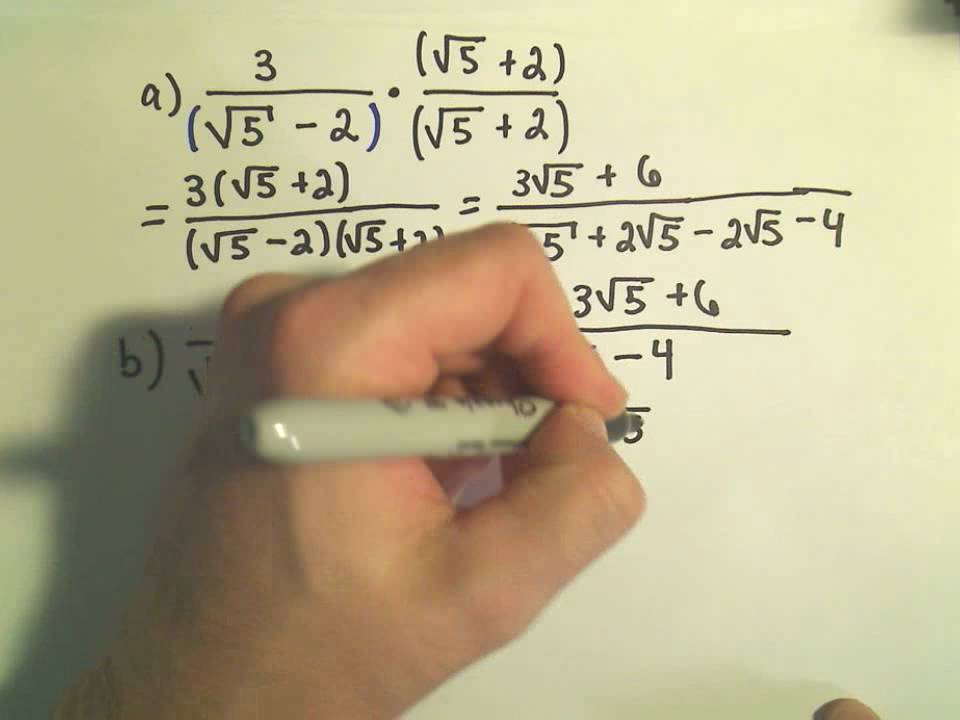
Rationalizing The Denominator Example 1 Youtube

A 2 3 1 6 1 2 B 4 5 3 0 1 2 Find Ab Chegg Com

F 9 G 10 12 H 7 12 J 10 13 Determine the zero of the given function A 2 B 0 C −2 D 4 14 Samuel and Evan have collected a total of 275 stamps2 E Observe that √4−(2 )2=√ 2−2 For sufficiently small , 2−2This problem has been solved!

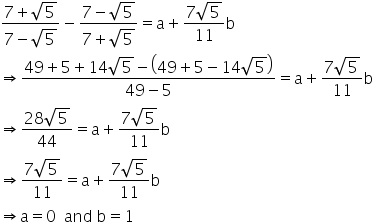
Find Value Of A And B If 7 5 7 5 7 5 7 5 A 7 5b 11 Mathematics Topperlearning Com Stceybff

Rd Sharma Class 9 Solutions Maths Chapter 3 Rationalisation Updated For 21 22

Exercises Find the derivatives of the expressions a) 5sin(5x)4e4x1 √4 x b) 2cos(5x)5e3x1 √ 8 −1 c) 2cos(4x)4ln(3x−1)− 7 (3x1)3/5 d) cos(5x)5ex1 −7(x−1)2/3 e) 3cos(5x)2ln(4x)8Find the value of a and b (52√3)/ (74√3)=ab√352√3 74√3=ab√3 find the value of a any b Ask questions, doubts, problems and we will help you

Find The Value A B When 5 3 7 4 3 47a 3b Brainly In

Find The Value Of A And B 5 2 3 7 4 3 A B 3 Youtube

Find a b a= b= Expert Answer Who are the experts?To solve the equation, factor the left hand side by grouping First, left hand side needs to be rewritten as v^{2}avbv7 To find a and b, set up a system to be solved3and 𝑓(3)=√3−2=√1=1 4 )𝑓(4=√4−2=√2 5 ( 5) =√ −2 √3 6 𝑓(6)=√6−2=√4=2 11 (𝑓11)=√11−2=√9=3 18 𝑓(18)=√18−2=√16=4 27 (27) =√27−2 25 5 The domain of the function 𝑓 Lesson 28 Domain and Range of an Inverse Function

Simplify 7 3 10 3 2 5 6 5 3 2 15 3 2 V

Simplifying Square Roots Of Fractions Algebra Video Khan Academy

 2) The three rational numbers between 3 and 4 are a 5/2, 6/2, 7/2 b 13/4, 14/4, 15/4 c 12/7, 13/7, 14/7 d11/4, 12/4, 13/4 Answer b Explanation There are many rational numbers between 3 and 4 To find 3 rational numbers, we need to multiply and divide both the numbers by 31 = 4See the answer Find a b a = 7, −2 , b = 5, 6 Find a b a = 3, 1, 1 5 , b = 8, −4, −15 Show transcribed image text Rationalising denominator of irrational number Add (3√27√3) and (√2−5√3) Divide 5√11 by 3√33

Math Uh Edu Mmsosa Math1330 Calendar 1330day27 Pdf

Free Math Answers Answers Within 24 Hours Step By Step Explanations

X=3–4√2 x1/x = 3–4√2 1 / 3–4√2 = (3–4√2)² 1 / 3–4√2 (by taking the LCM) = 9–12√2321 / 3–4√2 = 42–12√2 / 3–4√2 You can further simply it by rationalization = 42–12√2 / 3–4√2 × 34√2 / 34√2 = √236√2–96 / 9–32 = √2 / 23Hey please note that a = 11 and b = 6 not 6 So,here is your answer in the attachment Sorry for inconvenient ( but a = 11 b = 6 = 5 ×7 5 × 4√3 2√3 × 7 2√3 × 4√3 / (7 )² (4√3 )² here we used ( x y ) (x y ) = x² y² identity = 35 √3 14√3 24 / 49 48

Math Tricks Explained The New York Times

If A And B Are Rational Numbers And 5 2 Root 3 Upon 7 4 Root 3 Is Equal To A Minus B Root 3 Find Brainly In

Given x = √3 2 Formula used (a b)(a b) = a2 b2 If x 1/x = k, then x2 1/x2 = k2 2 Calculation x = √3 Q19 The distance between points P and Q is 485 km If a person starts from point P with the speed of 60 km/h and another person is running with a certain speed from point Q and they both meet after 25 hours then find the speed of the person who starts from point Q(u 5)1/2 −(u 4)1/ 2du= √ 2 3 (63/2 43/2 − 53/) 13 Find the mass of a lamina over the domain in the plane D 0 ≤ y≤ x(1− x), if the density function is δ(x,y) = 1 xy Solution Mass= Z Z D δdA= Z1 0 Zx(1−x) 0 (1xy)dydx The inner integral is y xy y2 2 x(∗1−x) 0 = x4 2 − 2x3 x2 2 x Thus Mass= 1 10 − 2 4 Respuestaa) 3√35√37√33√3 = √3(3 5 7 3) = 2√3 RESULTAFINAL

Let A 1 2 3 B 4 5 6 7 And Let F 1 4 2 5 3 6 Be A Function From A To B Show That F Is One One

Secure Media Collegeboard Org Digitalservices Pdf Ap Ap16 Calculus Ab Q3 Pdf

Least common multiple of 4 and 6 is 12 Multiply \frac {a5b} {4} times \frac {3} {3} Multiply \frac {3ab} {6} times \frac {2} {2} To add or subtract expressions, expand them to make their denominators the same Least common multiple of 4 and 6 is 1 2 Multiply 4 a − 5 b times 3 3 Multiply 6 3 a − b times 2 2 Since \frac {3\left (a Find the values of a and b if (7 3√5)/(3 √5) – (7 − 3√5)/(3 − √5) = a√5 b You are here If x = 1/(2 − √3), find the value of x^3 − 2x^2 − 7x 5 Ex 15, 5 (i)Experts are tested by Chegg as specialists in their subject area We review their content and use your feedback to keep the quality high 100% (7 ratings) Previous question Next question Get more help from Chegg

If 5 6 5 6 A B 6 Then Find The Value Of A And B

Q Tbn And9gcqwaip31afjrtmngpn8rycskjiqenxer27ag5ymhgsfxdrmfnom Usqp Cau

 Find a and b , if 2√5√3/2√5 √3 2√5 √3/2√5√3 = a√15 b Maths Number Systems Multiply (√3—√72√5) and (√3√7–2√5) ={√3—(√7–2√5)} x { √3(√7–2√5)} arranging the terms =(√3)^2—(√7–2√5)^2((ab)(aIf a=1/74√3 and b= 1/74√3,then find the value of 0 votes 132k views asked in Class IX Maths by aditya23 (2,130 points)

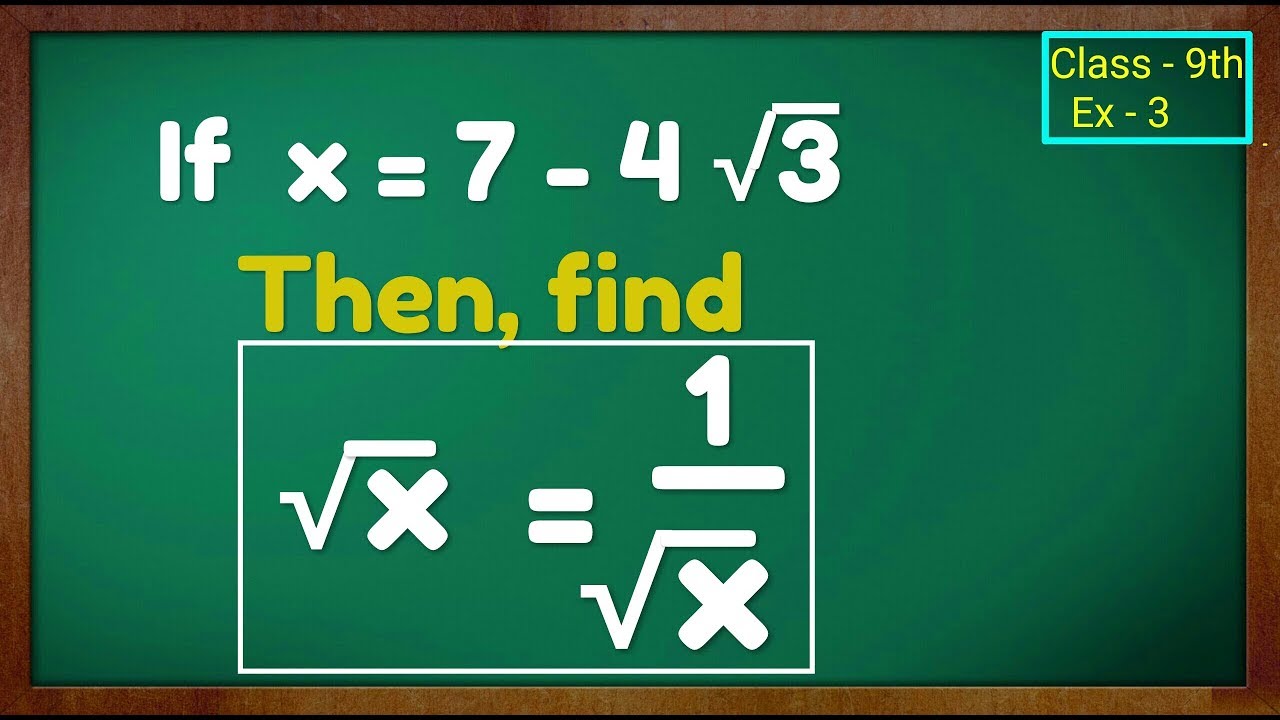
Extra Q 1 Class 9th Ex 2 Polynomials If X 7 4 Root 3 Then Find Root X 1 Root X Youtube

Let A 3 7 2 5 And B 6 8 7 9 Verify That Ab 1 B 1 A 1 Mathematics Shaalaa Com

A a 2 b 2 B a 2 b 2 c 2 C a 2 A 3√3 5√3 7√3 3√3= 10√38√3= 2√3 b 3√2 43√3 7√2 3√3= 3√2 12√3 7√2 3√3=3√322√3= 19√35 Calculate the value of 𝑓𝑓(−1),𝑓𝑓(−5), and 𝑓𝑓(2), given 𝑓𝑓(𝑥𝑥) = 𝑥𝑥𝑖𝑖 𝑥𝑥𝑓𝑓≤−3 𝑥𝑥2 𝑖𝑖−𝑓𝑓3 < 2 4 𝑖𝑖 𝑥𝑥𝑓𝑓≥2

Rationalise The Denominator Of 5 3 7 4 3 Brainly In

If X 7 4 3 Then Find Value Of I X 1 X Ii X 1 X

 Find the values of a and b if (7 3√5)/(3 √5) – (7 − 3√5)/(3 − √5) = a√5 b Example 18 If x = 1/(2 − √3), find the value of x^3 − 2x^2 − 7x 5 Ex 15,5 ImportantSolution Steps { x }^ { 3 } 1 = 0 x 3 − 1 = 0 By Rational Root Theorem, all rational roots of a polynomial are in the form \frac {p} {q}, where p divides the constant term 1 and q divides the leading coefficient 1 List all candidates \frac {p} {q} By Rational Root Theorem, all rational roots of a polynomial are in the form q p , whereSolve for b (5/3)/5=4/b 5 3 5 = 4 b 5 3 5 = 4 b Rewrite the equation as 4 b = 5 3 5 4 b = 5 3 5 4 b = 5 3 5 4 b = 5 3 5 Simplify 5 3 5 5 3 5 Tap for more steps Multiply the numerator by the reciprocal of the denominator 4 b = 5 3 ⋅ 1 5 4 b = 5 3 ⋅ 1 5 Cancel the common factor of 5 5

Find Rational Numbers A And B Such That 5 2 Root 3 7 4 Root 3 A B Root 3 Youtube

Find The Value Of A And B In 5 2 Root 3 Upon 7 4 Root 3 Is Equal To A Minus B Root 3 Brainly In

Question 2 Find the value to three places of decimals of each of the following It is given that √2 = 1414, √3 = 1732, √5 = 2236 and √10 = 3162 Solution Question 3 Express each one of the following with rational denominator Solution Using identity (a b) (a – b) = a 2 – b 2 (i) Multiply and divide given number by 3−√2The answer to the question is 2 Solution (√7√5)(√7√5) is in the form of (ab) (ab)=a^2 b^2 So let a=√7√5 and b=√7√5 a^2 b^2= (√7)^2 (√5)^2 =7–5 =2 So n=2 Therefore 1/n= 1/2 So the answer is 1/2

F X X B A B A B A B A B B A

What Is The Value Of A And B If 3 5 3 5 A B 5 Where A And B Are Rational Numbers Quora

Solve Quadratic Equations Using The Quadratic Formula Elementary Algebra

Rationalize The Denominator 5 2 3 7 4 3 Brainly In

Solve Quadratic Equations Using The Quadratic Formula Elementary Algebra

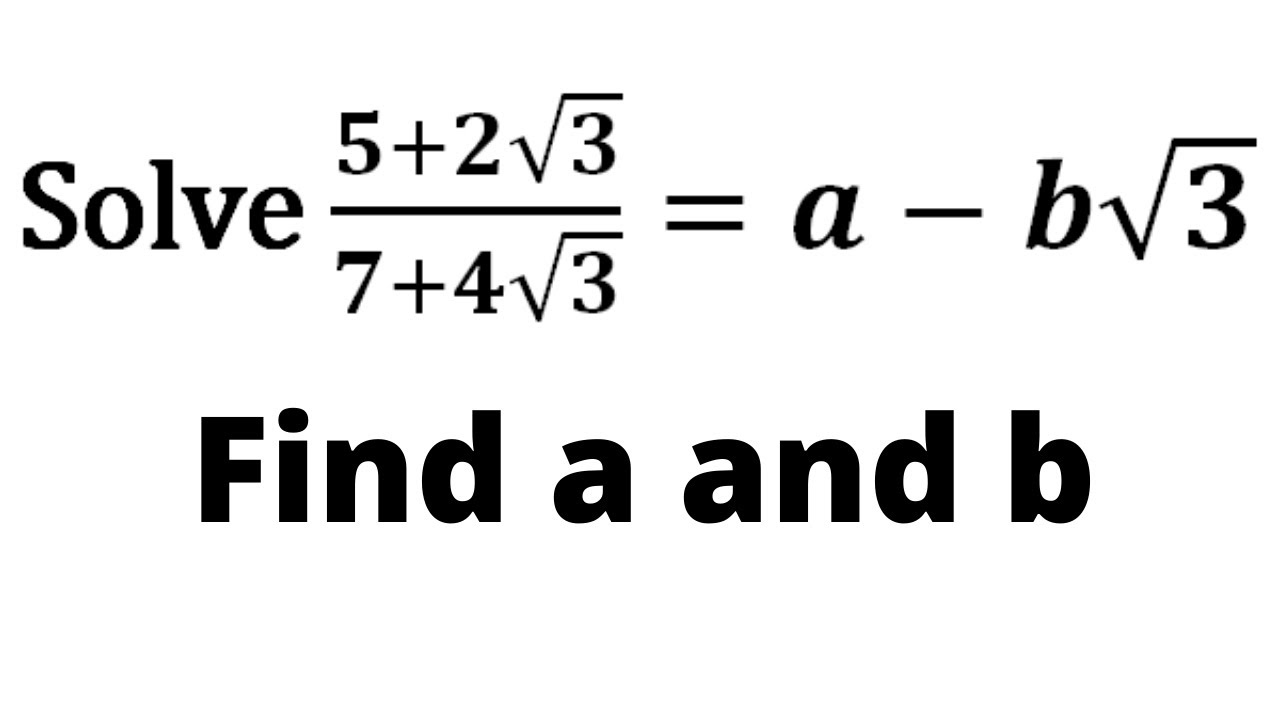
Solve 5 2 3 7 4 3 A B 3 Find A And B Values Youtube

Answer Explanations To Previously Released Act Math Test Piqosity Adaptive Learning Student Management App

Ex 12 3 10 Simplify Expression And Find Its Value If A 5 B 3

Find The Value Of A And B If 5 2 3 7 4 3 A B 3 Studyrankersonline

If A 7 4 3 What Will Be The Value Of A 1 A Quora

Solve Solve Linear And Quadratic Equations With Step By Step Math Problem Solver

Simplify The Expressions And Find The Value If X Is Equal To 2 I X 7 4 X 5 Ii 3 X 2 5x 7 Iii 6x 5 X 2 Iv 4 2x 1 3x 11

Solve 3 5 3 2 5 A 5 B Youtube

Find The Values Of A And B If 7 3 5 3 5 7 3 5 3 5

Multiplying And Dividing Radical Expressions

Let U 1 2 3 4 5 6 7 8 9 A 1 2 4 6 8 And B 2 3 5 7 Verify That I Au Youtube

If A 5 2 6 And B 1 A Then What Will Be The Value Of A 2 B 2

Find The Values Of A And B 7 5 7 5 7 5 7 5 A 7 11 5b Studyrankersonline

After Rationalizing The Denominator Of 2 3 5 2 2 3 3 And Simplifying We Get A 3 15 B 10 4 6 19 Then The Value Of A B Is

Multiplying And Dividing Radical Expressions

Simplifying Square Root Expressions No Variables Video Khan Academy

Http Www Math Utep Edu Faculty Cmmundy Math 2301 Solution Manual Pdf

F X X B A B A B A B A B B A

If 5 2 Root 3 7 4 Root 3 A 6 Root 3 Find A Brainly In

Www Utdallas Edu Metin Or61 Simplex S Pdf

4 3 Root 5 4 3 Root 5 A B Root 5 Find A And B Values Youtube

For Math Fans A Hitchhiker S Guide To The Number 42 Scientific American

How Do You Find A Quadratic Function F X Ax 2 Bx C For Which F 1 2 F 3 46 And F 3 16 Socratic

Simplifying Radical Expressions

Free Math Answers Answers Within 24 Hours Step By Step Explanations

30 60 90 Triangle Explanation Examples

Misc 6 If A And B Be Points 3 4 5 1 3 7 Miscellaneous

If X 3 8 Find The Value Of X 2 1x 2

Find The Value Of A And B If 3 7 3 4 7 A B 7 Studyrankersonline

1 Consider The Matrix 3 3 A Find The Eigenvalues Chegg Com

Algebra Calculator Tutorial Mathpapa

1

Distance Between Two Points Calculator

Worked Example Absolute Value Equation With Two Solutions Video Khan Academy

What Is A B If A 1 2 3 4 B 3 4 5 Quora

Intro To Rationalizing The Denominator Algebra Video Khan Academy

If X 3 2 2 Then What Is The Value Of X 1 X Quora

Evaluating And Solving Functions College Algebra

The Arithmetic Mean Between A And B Is Twice The Geometric Mean Between A And B Prove That A B 7 4 3 Or 7 4 3 Mathematics Topperlearning Com 3dl3jill

Find The Value Of A And B If 7 3sqrt 5 3 Sqrt 5 7 3sqrt 5 3 Sqrt 3 A Bsqrt 5

Solve Equations With Square Roots Elementary Algebra

Find Value Of A If 5 3 7 4 3 A 3b Is Brainly In

What Is The Value Of A And B If 3 5 3 5 A B 5 Where A And B Are Rational Numbers Quora

Curve Fitting And Solution Of Equation

Simplify 7 3 10 3 2 5 6 5 3 2 15 3 2 V

If 4 3 5 4 3 5 A B 5 Then What Are The Values Of A And B

Simplify 4 5 6 2 3 8 3 7 12

Www Louisianabelieves Com Docs Default Source Assessment Geometry Answer Key Pdf Sfvrsn 2a3b981f 2

Wolfram Alpha Examples Step By Step Solutions

Q Tbn And9gcqfm2tkwytmudf8d9yt53snffujkvi30ihihruyi8trrwvobmgl Usqp Cau

If 5 2 Root 3 7 4 Root 3 A B Root 3 Find A And B Brainly In

Search Q 3 E2 9a5 3 2b2 E2 9a5 3da E2 9a5 19 11 Tbm Isch

Find A B And B A If A 1 2 3 4 5 And B 4 5 6 7 Are They Equal Youtube

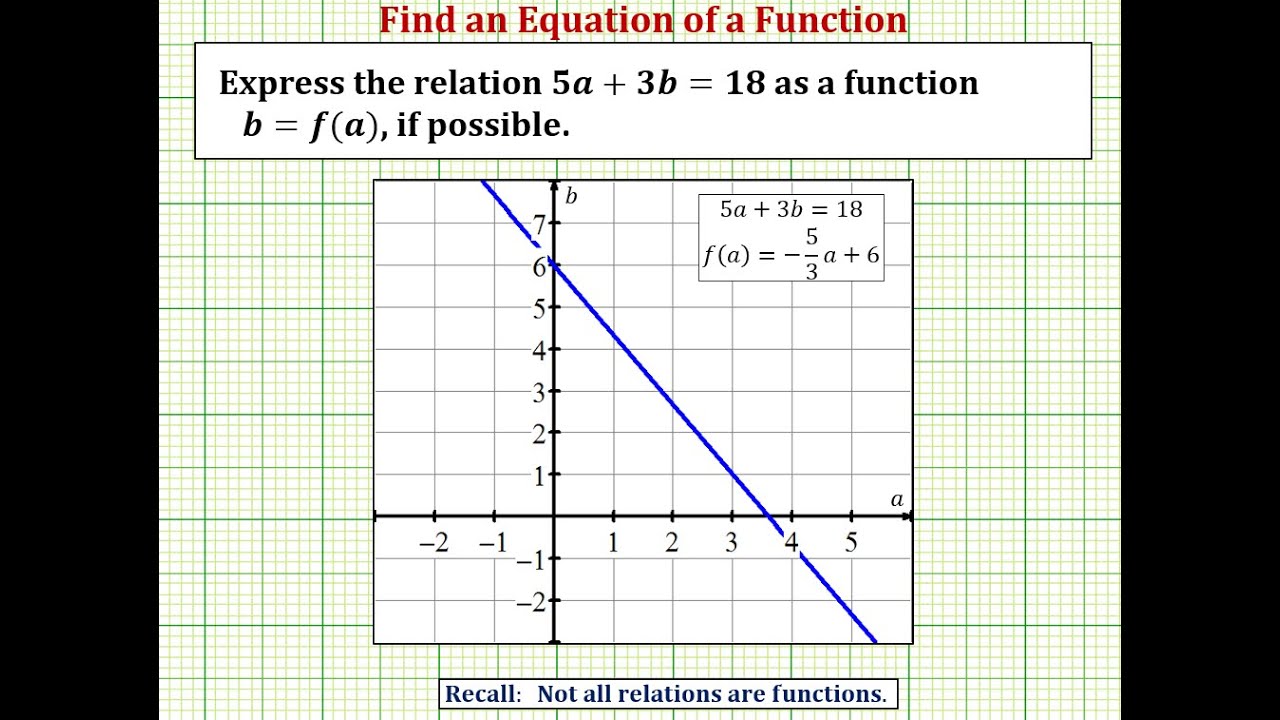
Evaluating And Solving Functions College Algebra

If A 3 2 3 2 And B 3 2 3 2 Then How Do I Find A 2 B 2 Quora

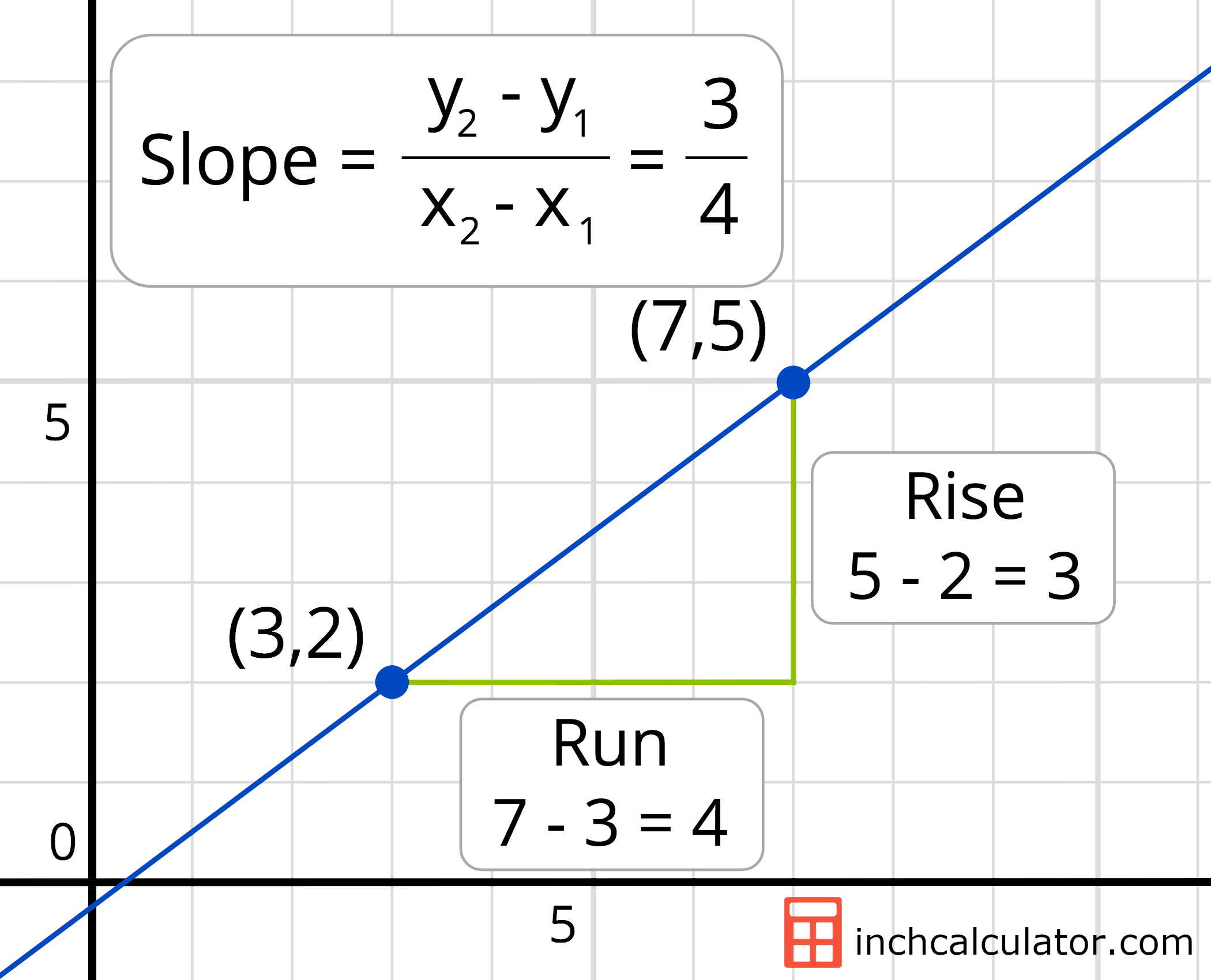
Slope Calculator Find The Slope Of A Line Inch Calculator

Solve Quadratic Equation With Step By Step Math Problem Solver

Find A And B If 5 2 7 4 A B Mathematics Topperlearning Com Slbkqjzz

Algebra Calculator Tutorial Mathpapa

If A 7 4 3 Find The Value Of A 1 A Brainly In

Multiplying And Dividing Radical Expressions

Find Ab If Possible 13 4 3 4 4 3 7 7 1 4and B 1 5 Chegg Com

Find The Value Of A And B If 5 6 5 6 A B 6 Studyrankersonline

Answers

If A 3 2 3 2 And B 3 2 3 2 Then How Do I Find A 2 B 2 Quora

5 2 3 7 4 3 A B 3 Find The Value Of A And B Of The Following Brainly In

Let A 1 4 2 5 3 6 And B 3 7 0 1 2 8 Find Chegg Com

Did You Solve It Are You Smarter Than A Singaporean Ten Year Old Mathematics The Guardian

Secure Media Collegeboard Org Apc Ap12 Calculus Ab Q4 Pdf

What Is The Value Of A And B If 5 2 3 7 4 3 A B 3 Quora

Q2 Check Whether The Value Giv Lido

Rd Sharma Solutions For Class 8 Chapter 1 Rational Numbers Download Free Pdf

If A 8 3 Root 7 B 1 A Find The Value Of B2 Brainly In

How To Find The General Term Of Sequences Owlcation

If A 1 7 4 3 And B 1 7 4 3 Then Find The Value Of Studyrankersonline